Vorbemerkung: In deiner Zeichnung hättest du einen anderen Buchstaben als a verwenden sollen, denn das a steht ja laut Aufgabenstellung bereits für die Seitenlänge des Quadrates. Ich werde statt dessen den Buchstaben d verwenden.
Ich nehme an, deine Frage lautet: Wie lang ist der Radius r zu wählen?
Nun, es gibt sicher einige Möglichkeiten, das zu bestimmen. Eine recht einfache habe ich im Bild skizziert:
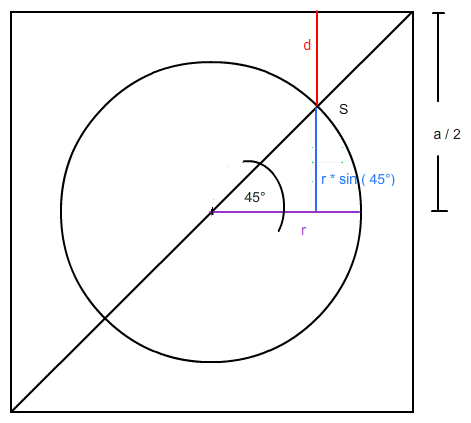
Gezeichnet ist ein Quadrat mit der Seitenlänge a. Die Diagonale dieses Quadrates bildet mit dem horizontal eingezeichneten Radius r (violette Strecke) einen Winkel von 45 ° Daher gilt für den als blaue Strecke eingezeichneten Abbstand des Schnittpunktes S zu diesem Radius:
r * sin (45°)
Die in rot eingezeichnete Strecke d ist der kürzeste Abstand von S zu einer der Seiten des Quadrates (entspricht der Strecke a in deiner Zeichnung).
Der Zeichnung ist zu entnehmen, dass gilt:
d + r * sin ( 45 ° ) = a / 2
Laut Aufgabenstellung soll gelten: d = 2 r , also:
2 r + r * sin ( 45 ° ) = a / 2
<=> r ( 2 + sin ( 45 ° ) = a / 2
<=> r = ( a / 2 ) / ( 2 + sin ( 45 °) )
<=> r = a / ( 4 + 2 * sin ( 45 ° ) )
und wegen sin ( 45° ) = 1 / √ 2
<=> r = a / ( 4 + 2 * 1 / √ 2 )
<=> r = a / ( 4 + √ 2 )
Bei einer Kantenlänge des Quadrates von a = 10 cm muss also der Radius
r = 10 / ( 4 + √ 2 ) ≈ 1,847 cm
gewählt werden, damit die Bedingung d = 2 r erfüllt ist.