Welchen Radius hat der Kreis um D, auf dem G liegt?

Question

ABCD sei ein Quadrat. K_A sei der Einheitskreis um A. EBFG sei ein Quadrat mit E auf K_A (siehe Abbildung):

Welchen Radius hat der Kreis K_D um D, auf dem G liegt?

Comments

[spoiler]

$$r_D = \sqrt{2}$$

[/spoiler]

---

Sollte R. dich (was zu erwarten ist) vor Erteilung einer Auszeichnung nach einer Begründung fragen, würde ich mit r_D =  | 1 - i | antworten.

---

Sollte R. dich (was zu erwarten ist) vor Erteilung einer Auszeichnung nach einer Begründung fragen, würde ich mit rD =  | 1 - i | antworten.

ich lasse die anderen erstmal vor. Darüber hinaus gibt es eine änlich einfache geometrische Begründung.

---

@Werner. Danke, dass du deine Antwort in einem nicht sofort sichtbaren Kommentar versteck hast. Mal sehen, ob überhaupt noch jemand antwortet. Meine kürzlich gestellte Matrixaufgabe blieb unbeantwortet, obwohl sie nicht schwerer war.

---

Da die Aufgabe weder eine konkrete Kantenlänge noch speziellen Forderungen an die konkrete Lage von E auf dem Einheitskreis macht kann man davon ausgehen, dass der gesuchte Radius von beiden unabhängig ist.

Wählt man für E die spezielle Lage auf der Strecke AB, hat G die spezielle Lage "Mitte des Viertelkreisbogens..."

Answer 1

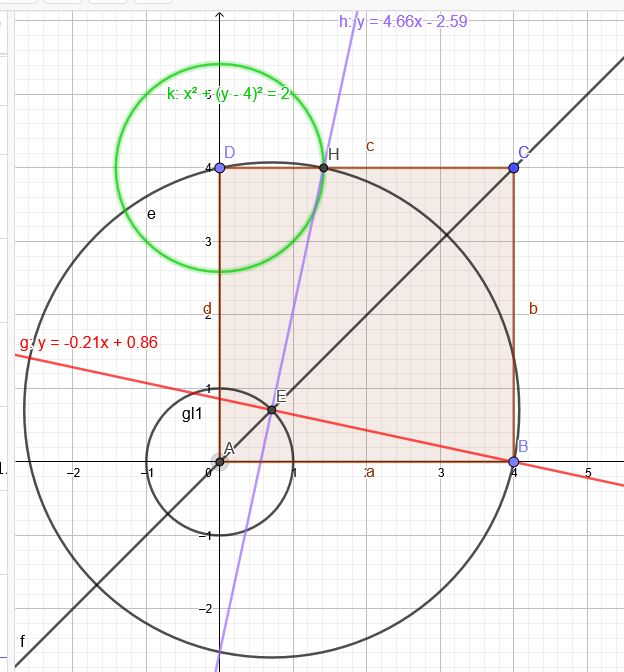
\(A(0|0), B(4|0),C(4|4),D(0|4)\)

Einheitskreis: \(x^2+y^2=1\)  geschnitten mit  \(y=x\)      \(E(\frac{1}{\sqrt{2}}|\frac{1}{\sqrt{2}})\)

Länge von Strecke EB:

\((4- \frac{1}{\sqrt{2}})^2+(\frac{1}{\sqrt{2}})^2=(EB)^{2} \)

\(16-\frac{4}{\sqrt{2}}+\frac{1}{2}+\frac{1}{2}=(EB)^{2} \)

\(16-\frac{8}{\sqrt{2}}+1=(EB)^{2} \)

\(16-4*\sqrt{2}+1=(EB)^{2} \)

\(EB=\sqrt{16-4*\sqrt{2}+1}≈3,36 \)

Gerade durch E und B:   \(y=-0,21x+0,86\)

Normale durch E:    \(y=4,66x-2,59\)

Kreis um E mit \(r^2=17-4*\sqrt{2}\) schneidet Normale in H.

Der Radius des Kreises um D beträgt nun \(r=\sqrt{2}\)

Comments

ich lasse die anderen erstmal vor

Jetzt siehst du, was du damit angerichtet hast

---

ich lasse die anderen erstmal vor
Jetzt siehst du, was du damit angerichtet hast

Tja - man kann machen was man willl, man macht es falsch ;-)

Answer 2

Nach meinem Kommentar von vorhin (Nutzung einer speziellen Lage) habe ich jetzt erst die Ähnlichkeit gesehen. Der grüne und der blaue Winkel bei B sind gleich, und BD:BA=BC:BE.

Dahinter steckt dann auch die Drehstreckung, wenn man es komplex möchte.

Comments

Nach meinem Kommentar von vorhin ist die ausführlichere Variante (kleine Buchstaben sind diejenigen kompexen Zahlen, deren Darstellung in der Ebene die mit den entsprechenden großen Buchstaben bezeichneten Punkte gemäß R.s Skizze sind, a=0)
|g-d| = | (i*(b-e) + e) - d | = | (i*b - i*e + e) - i*b | = | -i*e + e | = |e|*|-i + 1| = 1*√2