Ungleichungen mit quadratischer Funktion und Bruch

Question

Hi, ich habe hier eine Ungleichung bei der ich einfach nicht weiß, wie ich sie angehen soll:

5x² - 20x + 26 > 4/(x² - 4x +5)

Der "rechte Teil" ist eigentlich ein Bruch, keine Ahnung wie der einzufügen wäre.

Hab schon probiert mit | • (x² - 4x +5), um den Bruch aufzulösen und danach dann nach x hin aufzulösen, aber dann kommt am Ende nur x > 0 raus und das erscheint mir nicht richtig.

Danke schon einmal...

Comments

Hab schon probiert mit | • (x² - 4x +5), um den Bruch aufzulösen und danach dann nach x hin aufzulösen, aber dann kommt am Ende nur x > 0 raus

Können wir das mal sehen? Irgendwo muss doch ein Umformungsfehler stecken.

Answer 1

Hallo,

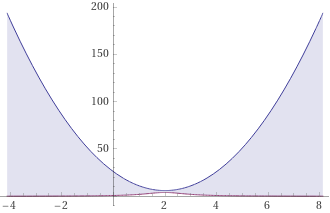
ich habe die beiden Terme graphisch dargestellt.

Blau: Linker Term

Rot: Rechter Term

Offensichtlich gilt die Ungleichung für alle reellen Werte von x.

Vielleicht reicht es zu zeigen, dass beide Terme bei x=2 ein globales Extremum haben und dass die Ungleichung dort erfüllt ist.

Jetzt habe ich es rechnerisch versucht:

5x² - 20x + 26 > 4/(x² - 4x +5)

(5x² - 20x + 26)(x² - 4x +5)>4

( 5(x-2)^{2}+6)((x-2)^2+1)>4

Die beiden Terme nehmen bei x=2 den kleinsten Wert an.

Für x=2:

6*1>4 ✓

Für alle anderen Werte ist die Ungleichung auch erfüllt.

:-)

Answer 2

5·x^2 - 20·x + 26 > 4/(x^2 - 4·x + 5)

Zum Glück hat der Nenner keine Nullstellen. Daher einfach mal multiplizieren

(5·x^2 - 20·x + 26)·(x^2 - 4·x + 5) > 4

5·x^4 - 40·x^3 + 131·x^2 - 204·x + 130 > 4

5·x^4 - 40·x^3 + 131·x^2 - 204·x + 126 > 0

Das scheint jetzt immer erfüllt zu sein.

Comments

Das scheint jetzt immer erfüllt zu sein.

Dieses Argument ist schwer zu toppen...

;-)

---

Rechnereinsetz liefert 4 komplexe Nullstellen. Aber man kann es auch anders zeigen. Das sei dem Fragesteller frei gestellt.

Erste Ableitung Null setzen gibt ein Minimum bei x = 2

Das Minimum bestimmen, welches mit 2 größer als 0 ist, sollte auch gehen.

---

Haha, ich habe tatsächlich etwas ähnliches herausbekommen. Ich glaube das Problem war einfach, dass ich mit > 0 am Ende nix anfangen konnte und gedacht habe, irgendwie ists komisch, wenn das für alle reellen x-Werte passt aber naja, muss ja danke an alle

Answer 3

Man kann das Ganze leicht auf die folgende Form bringen:

5 x⁴ -40 x³ + 131 x² - 204 x + 126 > 0

Mittels einer Kurvendiskussion der links stehenden Polynomfunktion vierten Grades kann man zeigen, dass die Ungleichung für alle reellen x-Werte erfüllt ist, da der absolute Minimalwert dieser Funktion positiv ist.

Comments

da der absolute Minimalwert dieser Funktion positiv ist.

Schöne Idee mit dem kleinen Haken, dass man erst einmal mit den nicht trivialen Nullsetzen einer Funktion dritten Grades eine Minimumstelle finden müsste...

---

Da hat man aber (unverdientes ?) Glück:  diese Ableitungsfunktion dritten Grades hat eine einzige und sehr einfach zu findende (ganzzahlige, kleine) Nullstelle !

Meiner Meinung ist das schon "trivial" für jemand, der mit dem Thema vertraut ist.