Wie gibt man hierbei die Mengen an? Ungleichungen mit Bruch und Betrag in R sowie Mengen in R^2.

Question

Ich bin total am Verzweifeln. .ich verstehe diese Aufgabe gar nicht ..ich weiß gar nicht wie ich vorangehen soll. .kann mir da jemand vielleicht behilflich sein?

M_(2) = { x Element R: |x+1| > 2 } n { x Element R : |x-1| <2 } 

Comments

Kann mir noch jemand erklären wie es bei 3) und 4) aussehen soll? Ich verstehe es einfach nicht. Habe ich es dort mit Vektoren zu tun?

---

Kannst du M_(3) einmal vorlesen?

Steht da

3 |y| < 9/2 |x| ?

Wolframalpha gibt dir an, was du zu erwarten hast:

https://www.wolframalpha.com/input/?i=3+%7Cy%7C+%3C+9%2F2+%7Cx%7C 

Zahlen kannst du im Link selber ändern.

Fallunterscheidungen wegen dem Betrag liefern dir die Begrenzungen y = 3/2 x und y = -3/2 x. Danach noch entscheiden in welchen Bereichen der Ebene die Ungleichung erfüllt ist und ob die Begrenzungen zum Gebiet gehören oder nicht (hier NICHT. D.h. die beiden Geraden nur gestrichelt einzeichnen.

Answer 1

M_(2) = { x Element R: |x+1| > 2 } n { x Element R : |x-1| <2 } 

Betrag einer Differenz bedeutet Abstand.

Daher erst mal Differenzen hinschreiben.

M_(2) = { x Element R: |x - (-1)| > 2 } n { x Element R : | x - 1| <2 } 

Nun Zahlenstrahl zeichnen.

 { x Element R: |x - (-1)| > 2 }

Alle Zahlen, die von (-1) einen Abstand mehr als 2 haben.

 { x Element R : | x - 1| <2 } 

Alle Zahlen, die von 1 einen Abstand von weniger als 2 haben.

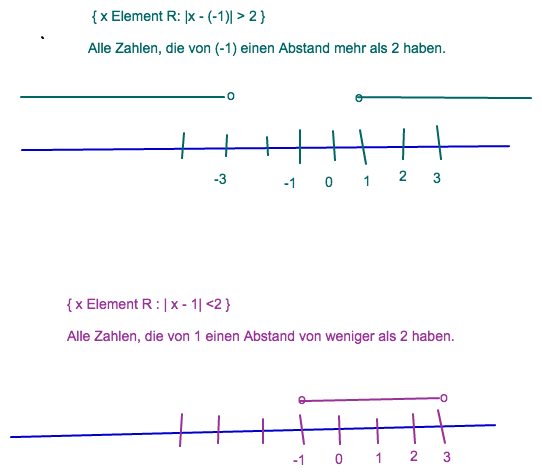
Zusammen: Durchschnitt bilden.

M_(2) = { x Element R: |x - (-1)| > 2 } n { x Element R : | x - 1| <2 } .

Wähle die Elemente des Zahlenstrahls, die in beiden Mengen liegen.

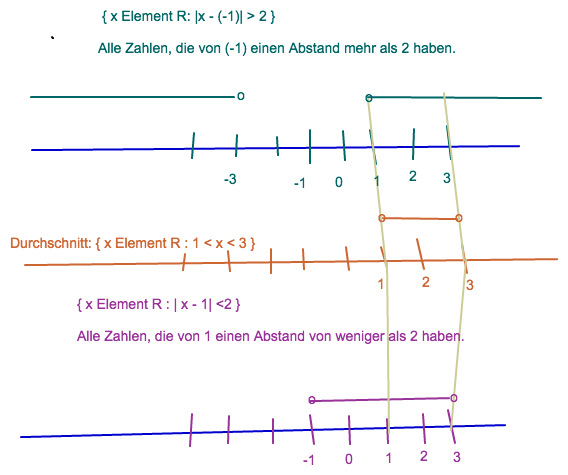
L = { x Element R | 1 < x < 3} 

Answer 2

Bei 1 musst du erst mal überlegen für welche x gilt

(2x-1) / (3x+1) > 4

Fallunterscheidung

1. Fall 3x+1>0 also   x > -1/3

dann hast du  (2x-1) > (3x+1) * 4

<=>   2x-1 > 12x + 4

<=>   -5 > 10x

also x < -1/2 wegen x > -1/3 ist das nicht möglich

2. Fall  3x+1<0 also   x<  -1/3

dann hast du  (2x-1) < (3x+1) * 4

<=>   2x-1 < 12x + 4

<=>   -5 < 10x

also x > -1/2 wegen x < -1/3 ist das das

offene Intervall von -1/2 bis -1/3.

Also ist dies die ganze Menge M₁ und die

Randpunkte gehören (wie immer bei

offenen Intervallen) nicht dazu.

Comments

Könntest du mir das bitte noch mal erklären? Ich weiß nicht wie ich diesen letzten Part -also x > -1/2 wegen x < -1/3 ist das das

offene Intervall von -1/2 bis -1/3.

Also ist dies die ganze Menge M₁ und die

Randpunkte gehören (wie immer bei

offenen Intervallen) nicht dazu.-  notieren soll . Und gibt es nicht eigentlich immer  Fälle? Ich habe das immernoch nicht drauf

Answer 3

Hi unknowni ! :-)

|x+1| > 2 ∩ |x-1| < 2

|x+1| > 2 ⇒ x ∈ (-oo, -3) ∪ (1, oo)
|x-1| < 2 ⇒ x ∈ (-1, 3)
|x+1| > 2 ∩ |x-1| < 2 ⇒ x ∈ (oo, -3) ∩ (1, oo) ∩ (-1, 3) = (1, 3)

Beste Grüße
gorgar

Comments

Ist das oo ein Unendlichzeichen , wenn ja warum? Und woher weißt du, dass das Ergebnis die Schnittmenge von 1 und 2 sind? Und warum 1 und 3 ? Denn es sind zwar die Zahlen vorhanden, aber in jeder Klammer mit einem anderen Vorzeichen.

---

Ist das oo ein Unendlichzeichen

Ja, so ist es. Das macht man so mit zwei o hintereinander, wenn gerade kein Unendlichkeitszeichen verfügbar ist oder aus Faulheit. :-O

wenn ja warum?

Weil das die Ergebnisse der Teilaufgabe sind.
Wenn die Lösungsmenge z.B.  x < -3 ist, dann kann man das in Intervallschreibweise so schreiben: x ∈ (-oo, -3) ^(*)

Und woher weißt du, dass das Ergebnis die Schnittmenge von 1 und 2 sind?

Weil das die Aufgabenstellung hergibt. Das kannst du am Zeichen ∩ für Schnittmenge erkennen. https://www.mathebibel.de/schnittmenge

Und warum 1 und 3 ?

Das ist das Ergebnis. Das ist die Schnittmenge der drei Intervalle (-oo, -3), (1, oo), (-1, 3). Mach Dir das vielleicht mal anhand des Zahlenstrahls klar - So wie es  Lu in seinem graphischen Lösungsweg vorgeführt hat, den ich deutlich einfacher und eleganter als meinen finde.

^(*)
Gerade ist mir beim Antworten ein Fehler aufgefallen: Ich hate (oo, -3) geschrieben, das ist natürlich Stuss. Es muss (-oo, -3) sein. Habe es verbessert.

---

Vielen Dank`!

Könntest du mir vielleicht noch sagen, wie man bei 3) und 4 ) vorangeht ? Sind es Vektoren? Kann ich mir irgendwie schlecht vorstellen

---

Könntest du mir vielleicht noch sagen, wie man bei 3) und 4 ) vorangeht ? Sind es Vektoren?

Ja, so ist es. Die Lösungsmenge ist eine gewisse Menge von Vektoren.


Kann ich mir irgendwie schlecht vorstellen

Ja, ich auch. Ohne Zeichnung kann ich mir das sogar gar nicht vorstellen.


3)
Eine Äquivalenzumformung als Vorbereitung könnte helfen: 3|y| < 9/2|x| <=> |y| < 3/2|x|

y,x können jeweils positiv oder negativ sein, d.h. es gibt 4 Möglichkeiten:

1) y > 0
1.1) x > 0 => y < 3/2x
y > 0 und y < 3/2x
1.2) x < 0 => y < -3/2x
y > 0 und y < -3/2x

Analog
2) y < 0
2.1) x > 0  => y > -3/2x
y < 0 und y > -3/2x
2.2) x < 0 => y > 3/2x
y < 0 und y > -3/2x

Wir können zwei Geradengleichungen erkennen: f: y = 3/2x und g: y = -3/2x
Die Geradengleichungen können wir zeichnen und anschließend die vier Möglichkeiten 1.1), 1.2), 1.3) und 1.4) kennzeichnen. Habe die 4 Bereiche bunt gemacht, damit Du sie besser zuordnen kannst.