Aufgabe:

Text erkannt:
Aufgabe \( 6^{\star}: \) Das cartesische Produkt
$$ \mathbb{R}_{n}:=\underbrace{\mathbb{R} \times \mathbb{R} \times \cdots \times \mathbb{R}}_{n \text { -mal }}=\left\{\left(a_{1}, a_{2}, \ldots, a_{n}\right) \mid a_{i} \in \mathbb{R}\right\} $$
kann auch als Spalte geschrieben werden:
$$ \mathbb{R}^{n}:=\underbrace{\mathbb{R} \times \mathbf{R} \times \cdots \times \mathbb{R}}_{n \text { -mal }}=\left\{\left(\begin{array}{c} a_{1} \\ \vdots \\ a_{n} \end{array}\right) \mid a_{i} \in \mathbf{R}\right\} $$
Das cartesische Produkt
$$ \begin{aligned} \mathbb{R}_{n}^{m} &:=\underbrace{\mathbb{R}_{n} \times \mathbb{R}_{n} \times \cdots \times \mathbb{R}_{n}}_{m \text { -mal }}=\left\{\left(\begin{array}{c} \left(a_{11}, a_{12}, \ldots, a_{1 n}\right) \\ \left(a_{21}, a_{22}, \ldots, a_{2 n}\right) \\ \vdots \\ \left(a_{m 1}, a_{m 2}, \ldots, a_{m n}\right) \end{array}\right) \mid\left(a_{i 1}, a_{i 2}, \ldots, a_{i n}\right) \in \mathbb{R}_{n}\right\} \\ &=:\left\{\left(\begin{array}{cccc} a_{11} & a_{12} & \ldots & a_{1 n} \\ a_{21} & a_{22} & \ldots & a_{2 n} \\ \vdots & \vdots & & \vdots \\ a_{m 1} & a_{m 2} & \ldots & a_{m n} \end{array}\right) \mid a_{i j} \in \mathbb{R}\right\} \end{aligned} $$
ist die Menge aller \( (m \times n) \) -Matrizen. Mit der skalaren Multiplikation und der Addition für Matrizen ist auf \( \mathbb{R}_{n}^{m} \) eine äußere und innere Verknüpfung erklärt. \( \left(\mathbb{R}_{n}^{m},+, \odot\right) \) ist ein Vektorraum. Zeigen Sie, dass das Distributivgesetz \( 2\left(S_{3}\right) \) gilt. Geben Sie an, an welcher Stelle Sie die Körperaxiome der rellen Zahlen verwenden.
Lösung: 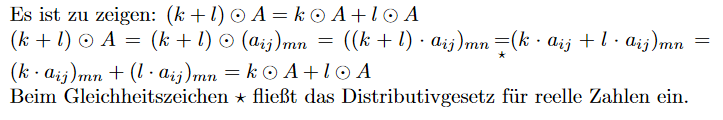
Text erkannt:
Es ist zu zeigen: \( (k+l) \odot A=k \odot A+l \odot A \) \( (k+l) \odot A=(k+l) \odot\left(a_{i j}\right)_{m n}=\left((k+l) \cdot a_{i j}\right)_{m n}=\left(k \cdot a_{i j}+l \cdot a_{i j}\right)_{m n}= \)
\( \left(k \cdot a_{i j}\right)_{m n}+\left(l \cdot a_{i j}\right)_{m n}=k \odot A+l \odot A \)
Beim Gleichheitszeichen \( \star \) fließt das Distributivgesetz für reelle Zahlen ein.
Problem/Ansatz:
Kann mir jemand erklären, wass genau gemaacht werden muss und wie man auf das Ergebnis kommt?
Und was ist mit innerer und äußerer Verknüpfung gemeint?
VIelen Dank !