Strahlensätze Text aufgaben

Question

Aufgabe:

a) Erläutere die Vorgehensweise.

b) Zeichne in ein gleichschenkliges Dreieck ein möglichst großes Quadrat ein. Nutze dabei die Idee, die in Fig. 3 dargestellt ist.

c) Suche nach weiteren Möglichkeiten, ein möglichst großes Quadrat in ein gleich-

Answer 1

Hallo,

Zeichne in das gleichschenklige Dreieck \(\triangle ABC\) (mit Basis \(AB\)) zunächst ein beliebiges Quadrat ein, so dass seine beiden oberen Ecken auf den Schenkeln des Dreiecks liegen und ein Paar Seiten des Quadrats parallel zur Grundseite des Dreiecks verläuft.

Führe dann, ausgehend von \(C\), eine zentrische Streckung des Quadrats durch.

Die beiden Strahlen durch die unteren Ecken des Ausgangsquadrats schneiden die Grundseite \(AB\) des Dreiecks in den unteren Ecken des gesuchten Quadrats.

Gruß Werner

Comments

Hier https://www.mathelounge.de/610339 hatten wir schon mal ein ähnliches Thema.

---

noch ein Goodie zur Teilaufgabe c). Das funktioniert für beliebige Dreiecke!

Im Dreieck \(\triangle ABC\) soll ein Quadrat auf der Grundseite \(c\) eingezeichnet werden.

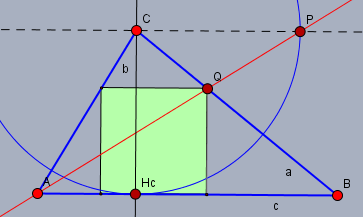
Schlage dazu einen Kreis mit dem Radius der Höhe \(h_c\) um \(C\). Dieser Kreis schneidet die Parallele (schwarz gestrichelt) zu \(c\) durch den Punkt \(C\) in zwei Punkten. Der Punkt, der auf der Seite von \(B\) liegt, sei \(P\). Die Gerade durch \(AP\) (rot) schneidet die Seite \(BC=a\) in \(Q\).

\(Q\) ist eine obere Ecke des gesuchten Quadrats.