Stochastik Winkelveränderung

Question

Aufgabe:

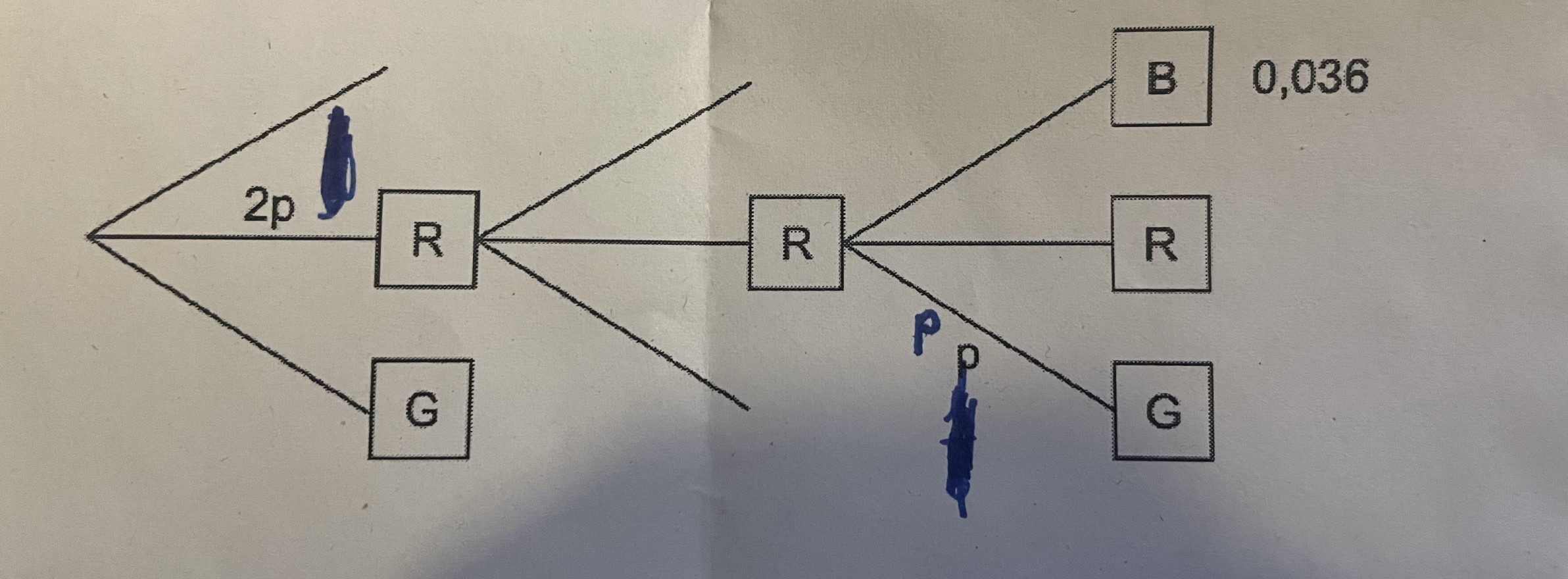
Die Größe der Sektoren werden geändert. Dabei wird der blaue Sektor vergrößert. Die Abbildung zeigt einen Teil eines Baumdiagramms, das für das geänderte Glücksrad die drei Drehungen beschreibt. Ergänzend ist für einen Pfad die zugehörige Wahrscheinlichkeit angegeben.

Bestimmten Sie die Größe des zum blauen Sektor gehörenden Mittelpunktwinkels.

R= rot, B=blau, G=grün

RRB=0,036

Problem/Ansatz:

Die vorigen Sektoren und die zugehörigen Mittelpunktswinkel sind B=180Grad, R=120Grad und G=60Grad.

Nun soll B größer werden. Laut den Ausgangswinkeln ist die Wahrscheinlichkeit RRB= 1/18

Answer 1

Du hast ein Gleichungssystem

I:       r*r*b = 36/1000

II:      2*g = r

III:     r+g+b = 1

Die Lösung

\( b=\frac{1}{10}, \quad g=\frac{3}{10}, \quad r=\frac{3}{5} \)

ist nicht die gesuchte, denn da steht noch "Nun soll B größer werden" und wenn man das Gleichungsystem für die alte Aufteilung des Glücksrades aufstellt, ist "grösser werden" gegenüber jenen Lösungen (die man ausrechnen könnte aber nicht muss, weil die alten Winkel ja angegeben werden) nur mit der zweiten Lösung möglich.

Comments

1. wie rechne ich das Gleichungssystem

2. blau hat einen Winkel von 180Grad nun soll der ja größer werden, aber bei dir ist der jetzt kleiner..

---

Bei mir ist der Winkel des blauen Sektors nicht kleiner:

nur mit der zweiten Lösung möglich

Lösen würde ich das Gleichungssystem mit Taschenrechner & Co. Bei mir zeigt der Rechenknecht an:


Die erste Lösung kann man verwerfen, weil es keine negativen Wahrscheinlichkeiten gibt, die zweite ist die von mir erwähnte Lösung (mit b > 0.5)

---

Der blaue Sektor muss aber größer als 0.5 sein laut der Aufgabe. Aber 0.1 ist ja kleiner als 0.5

---

die zweite ist die von mir erwähnte Lösung

Dort steht b = 0,64586...

---

Ach da tut mir leid. Wie kommt man aber mit Rechenwegen auf dieses Ergebnis?

---

zum Beispiel so:

II: g = r/2

II in III eingesetzt: r + r/2 + b = 1

b = 1 - 1,5r

das in I eingesetzt: r * r * (1-1.5r) = 36 / 1000

r² - 1,5r³ = 36 / 1000

Lösungen: r₁ ≈ -0.169425, r₂ ≈ 0.236092, r₃ = 0.6

Das jeweils in I eingesetzt ergibt die drei Lösungen für b und jeweils in II eingesetzt die Lösungen für g.