Berechnen Sie den Winkel alpha im Bogenmaß.

Question

Text erkannt:

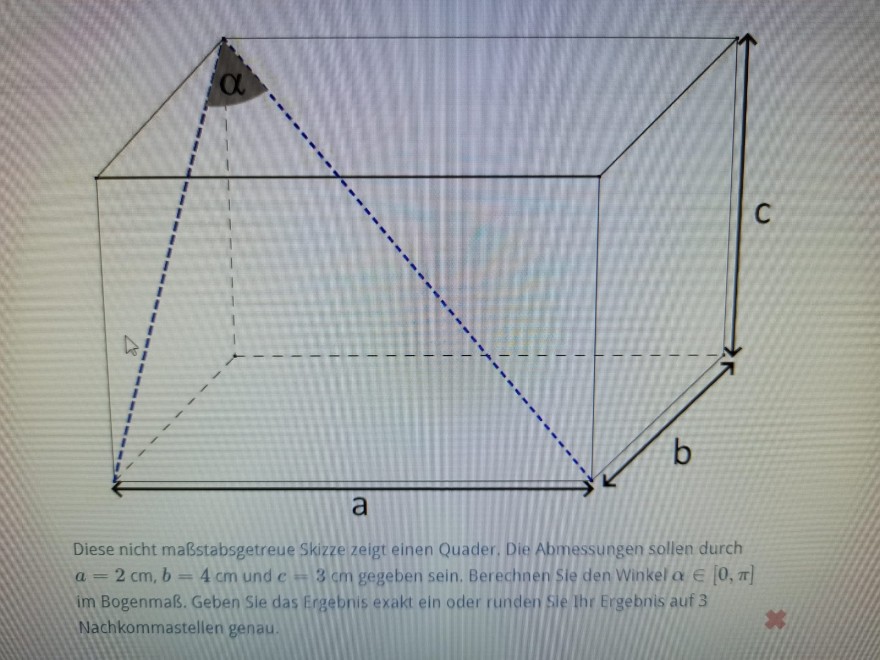
Diese nicht maBstabsgetreue Skizze zeigt einen Quader, Die Abmessungen sollen durch \( a=2 \mathrm{~cm}, b=4 \mathrm{~cm} \) und \( c=3 \mathrm{~cm} \) gegeben sein. Berechnen Sle den Winkel \( \alpha \in[0, \pi] \) im Bogenmaß. Geben Sie das Ergebnis exakt ein oder runden Sie Ihr Ergebnis auf 3 Nachkommastellen genau.

Aufgabe:

Diese nicht maßstabsgetreue Skizze zeigt einen Quader, Die Abmessungen sollen durch \( a=2 \mathrm{~cm}, b=4 \mathrm{~cm} \) und \( c=3 \mathrm{~cm} \) gegeben sein. Berechnen Sle den Winkel \( \alpha \in[0, \pi] \) im Bogenmaß. Geben Sie das Ergebnis exakt ein oder runden Sie Ihr Ergebnis auf 3 Nachkommastellen genau.

Problem/Ansatz:

Ich habe die Flaeche als rechtwinklinges Dreieck gesehen durch den rechten Winkel unten links.

Die Ankathete hab ich berechnet als x = \( \sqrt{3^2+4^2} \)

Also, ich habe die Hypotenuse als Raumdiagonale des Quaders ausgerechnet

d = \( \sqrt{3^2+2^2+4^2} \) = \( \sqrt{29} \)

Mit sin^-1  = 2/\( \sqrt{29} \) komm ich auf 0,3805 gerundet = 0,381.

Stimmt das Ergebnis und kann man anders bzw. schneller vorgehen?

Comments

Stimmt das Ergebnis   Ja

und kann man anders bzw. schneller vorgehen?   Benutzung von tan erspart Berechnung von d

---

Gradmaß ins Bogenmaß:

a = Winkel im Gradmaß

b = Winkel im Bogenmaß

a/360° = b/(2*pi)

b= a*pi/180

Answer 1

Lege den Quader in ein Koordinatensystem:

\( \vec{CA} \)=\( \begin{pmatrix} 0\\-4\\-3 \end{pmatrix} \)und \( \vec{CB} \)=\( \begin{pmatrix} 2\\-4\\-3 \end{pmatrix} \).

Dann gilt cos(α)=\( \frac{\vec{CA}·\vec{CB}}{|\vec{CA}|·|\vec{CB}|} \).