Integralfunktion und Stammfunktionen

Question

Hallo,

Ich habe die Funktion f(x)=x*(x-1)*(x-3) gegeben.

Meine Frage ist nun: Welche Stammfunktion von f kann keine Integralfunktion zu f sein?


vielen Dank im Voraus:)

Comments

F ist eine Stammfunktion von f , falls  F' = f

Aber was genau verstehst du unter einer "Integralfunktion" der gegebenen Funktion f ?

Answer 1

Jede Integralfunktion ist eine Stammfunktion, aber nicht jede Stammfunktion ist eine Integralfunktion, da Integralfunktionen eine Nullstelle besitzen müssen.

Ausgangsfunktion f(x)

Stammfunktion F(x), mit F'(x)=f(x)

Integralfunktion:

\( I_a(x)=\int\limits_a^x f(t)dt=F(x)-F(a)\)

Dabei gilt I(a)=0.

Stammfunktionen, die keine Nullstelle haben, sind deshalb keine Integralfunktionen.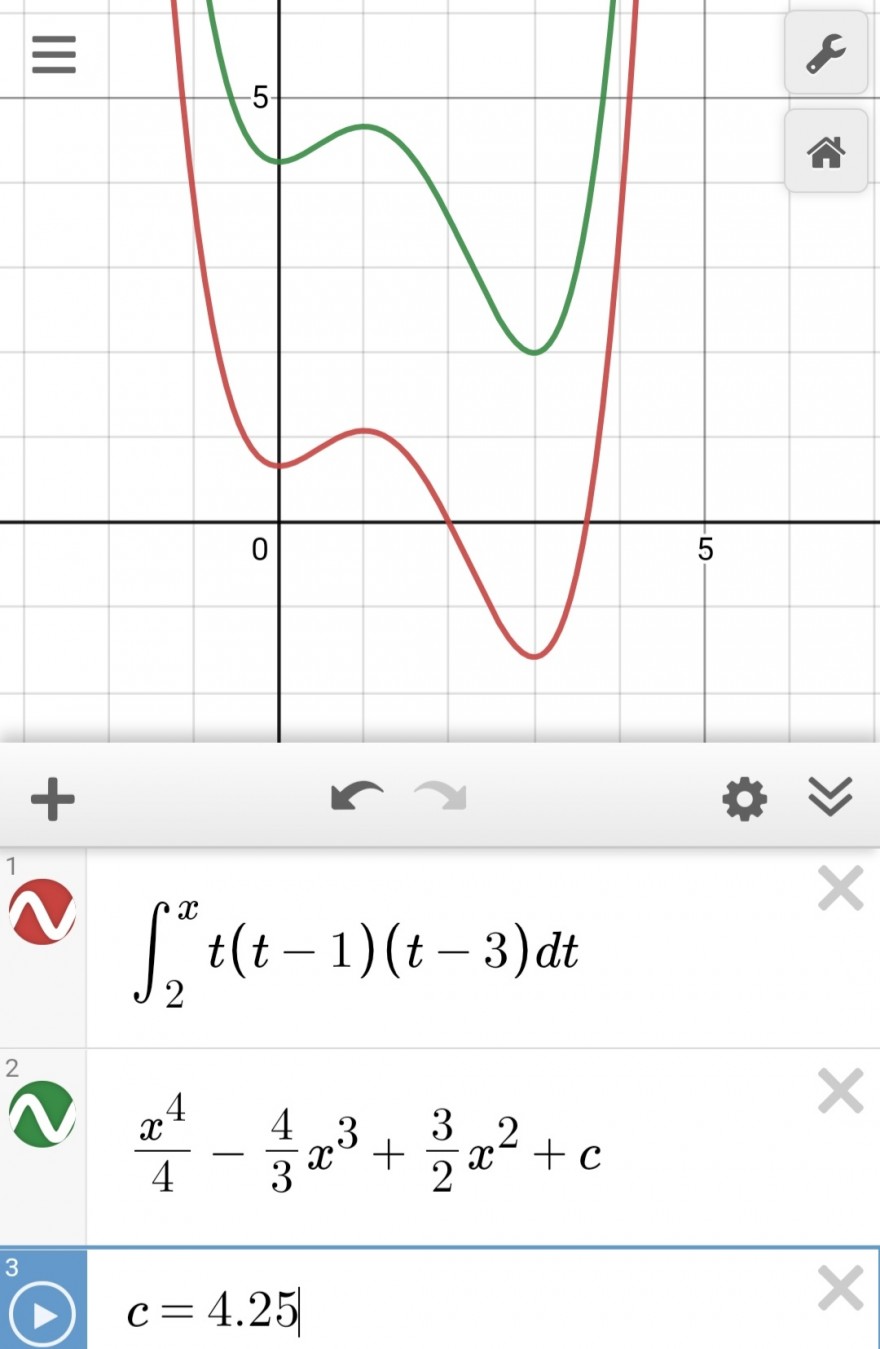

Rot: Integralfunktion

Grün: keine Integralfunktion

:-)