Wie finde ich Seite b

Question

Aufgabe:

Wie kann man mit denn sinussatz die Höhe eines Dreiecks herausfinden Aufgabe: a=26

c=6 alpha 62 grad

Betta=90

Gamma = 28grad

Die Seite b also die Länge wird gesucht

…

Problem/Ansatz:

Comments

Hast du die Angaben richtig abgetippt?

---

Nein habe mich vertippt Schuldige also die richtige Aufgabe ist :ich soll die Höhe eines gleichschenkligen Trapez mit dem sinussatz herausfinden.Gegeben ist alpha =62grad Gamma=28 Beta=90 a=26 c=6 und die Seite b ist Gesucht

---

Ist das die gleiche Frage, die du vor ein paar Tagen schon gestellt hast und die von lul beantwortet wurde?

---

ich soll die Höhe eines gleichschenkligen Trapez mit dem sinussatz herausfinden.Gegeben ist alpha =62grad Gamma=28 Beta=90 a=26 c=6

In einem gleichschenkligen Trapez gilt \(\alpha = \beta\). Das ist bei Dir nicht der Fall!

Für die Berechnung der Höhe in einem Trapez brauchst Du normalerweise nicht den Sinussatz. Sind in einem gleichschenkligen Trapez \(\alpha\), \(a\) und \(c\) gegeben. so gilt für die Höhe \(h\)$$\tan \alpha = \frac{h}{\frac 12(a-c)} \implies h = \frac 12(a-c) \tan \alpha$$

---

Danke das hat mir echt weiter geholfen !:)

---

Meine Frage wäre noch ob diese Formel selbst umgestellt wurde oder eine feste Formel ist ?

---

Betrachte das rechtwinklige Dreieck AFD und wirf einen Blick in deine Formelsammlung. Dort steht bei Beziehungen im rechtwinkligen Dreieck unter anderem

\( \tan \alpha=\frac{a}{b}=\frac{\text { Gegenkathete von } \alpha}{\text { Ankathete von } \alpha} \)

Die Gegenkathete von alpha ist die Strecke DF = h = Höhe des Trapezes und die Ankathete die Strecke AF = \(\frac{1}{2}(a-c)=\frac{1}{2}(26-6)=10\)

---

Meine Frage wäre noch ob diese Formel selbst umgestellt wurde oder eine feste Formel ist ?

Oh je! - was verstehst Du denn unter einer "festen Formel"?

Danke das hat mir echt weiter geholfen !:)

Ich hoffe nur, diese Aussage bezieht sich auf die Skizze und nicht auf

\(h=(a-c)/2 \cdot \tan \alpha\) ;-)

Tipp: versuche nicht irgendwelche 'Formeln' zu lernen, sondern Zusammenhänge zu verstehen. Die einzige "Formel", die Du für obige Aufgabe kennen musst, ist$$\tan \alpha = \frac{\text{Gegenkathete}}{\text{Ankathete}}$$(s. Kommentar von Silvia). Der Rest folgt logisch(!) aus der Skizze und z.B. aus dem Wissen, dass in einem Parallelogramm benachbarte Seiten gleich lang sind.

Und damit man das hinkriegt, braucht man in jedem Fall eine Skizze; und keine Formel!

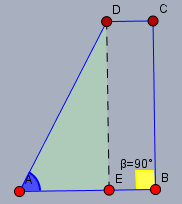
Btw.: bist Du sicher, dass das Trapez gleichschenklig und nicht rechtwinklig ist? Mit \(\beta = 90°\) wäre letzteres nämlich der Fall! Und dann sähe die Skizze so aus

Answer 1

zuerst immer eine Zeichnung machen.

Aus der Zeichnung kann man alle Seiten und Winkel ausmessen → die Genauigkeit liegt da bei +/- 2%

Dann rechnet man das Ganze nochmal nach

hier ist ein Winkel 90° → ein rechtwinkliges Dreieck

sin(a)=Gk/Hy

cos(a)=Ak/Hy

tan(a)=Gk/Ak

c²=a²+b²

Mir ist unklar,was da nun genau gesucht wird.

Merke:Für jede Unbekannte braucht man eine Gleichung,sonst ist die Aufgabe nicht lösbar.

Ausnahme:Man hat 3 Unbekannte und nur 2 Gleichungen.Beide Gleichungen nach einer Unbekannten umstellen und dann gleichstzen.Wenn man Glück hat,dann haben sich 2 Unbekannte auf und man hat nur noch eine Unbekannte und 1 Gleichunge,also lösbar