Gauß-Algorithmus anwenden.

Question

Aufgabe:

Hi, Ich soll auf folgendes LGS den Gauß Algorithmus anwenden.

2x +4y -3z = - 9

3x - 1y +3z = - 5

-3x -13y +12z = 22

Hab ich gemacht und als Ergebnis rausbekommen, dass das LGS unendlich viele Lösungen hat, weil de letzte Zeile gleich 0 ist.

I     6 • x + 12 • y - 9 • z = - 27

II             14 • y - 15 • z = - 17

III    0                              = 0

Problem/Ansatz:

Ich habe die freie Variable z = t gesetzt und in die zweite Gleichung eingesetzt und umgeformt und die 2. "neue" Gleichung dann in die 1. Gleichung eingesetzt. Meine Lösungsmenge ist wie folgt :

L = { \( \frac{-29}{14} \) - \( \frac{9}{14} \) * t ,  \( \frac{-17}{14} \) + \( \frac{15}{14} \) *t , t   Ι  t ist eine Zahl aus R}

In den offiziellen Lösungen ist diese Lösung jedoch nicht angegeben und ich verstehe nicht wo ich einen Fehler gemacht habe.

Hier die offiziellen Lösungsmöglichkeiten :

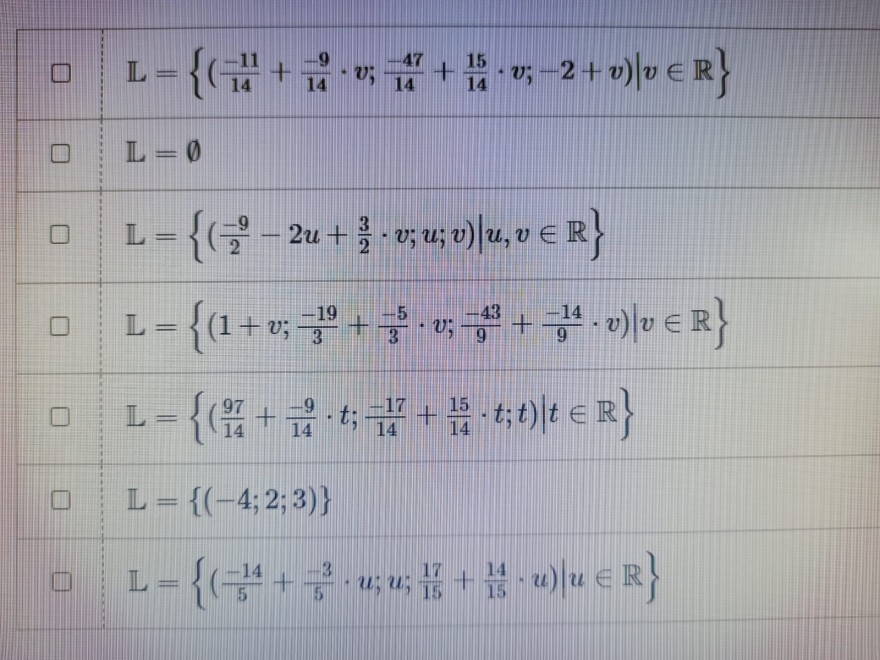
Eine oder mehrere Antworten sind richtig, leider deckt sich keine mit meiner errechneten Lösung.

Comments

Erfüllt deine Lösung deine erhaltene Stufenform?

Erfüllt deine Lösung das originale System?

Answer 1

Hallo,

du hast richtig gerechnet.

Etwas eigenartig ist die mittlere Lösung, die laut Wolframalpha richtig ist.

\( x=v+1,\\ y=-\frac{5 v}{3}-\frac{19}{3}\\  z=-\frac{14 v}{9}-\frac{43}{9} \)

Richtig ist auch die erste:

\( x=-\frac{9 v}{14}-\frac{11}{14}, \quad\\ y=\frac{15 v}{14}-\frac{47}{14}, \quad\\ z=v-2\)

und die letzte:

\( x=-\frac{3 u}{5}-\frac{14}{5}, y=u, z=\frac{14 u}{15}+\frac{17}{15} \)

Die anderen Vorschläge müssten falsch sein.

:-)

Answer 2

Das System hat die Lösungen x = -13, y = 17, z = 17.

Wahrscheinlich ist 3x - 1y +3y = - 5 ein Schreibfehler.

Comments

Ja hab mich vertippt habe es korrigiert jetzt.

Answer 3

Falls der Gauß-Algorithmus nicht verlangt ist:

1.) 2x +4y -3z = - 9

2.) 3x - 1y +3z = - 5  → y=(3x+3z+5 )  ∈  1.)+2.): 5x+3*(3x+3z+5 ) =-14 → A) 14x+9z =-29

3.) -3x -13y +12z = 22

1.)+2.): 5x+3y=-14

2.)+3.):  -14y+15z=17      2.) y=(3x+3z+5 ) ∈  2.)+3.): -14*(3x+3z+5 ) +15z=17 → -42x-27z =87→B)-14x-9z=29

A) 14x+9z =-29

B)-14x-9z=29

A)+B): 0