Vollständige Induktion 1/(n*(n + 2))=n*(3*n + 5)/(4*(n + 1)*(n + 2))

Question

Aufgabe:

Text erkannt:

Aufgabe 1:
Vollständige Induktion
Beweisen Sie, dass für alle natürlichen Zahlen n die folgende Summenformel gilt:
\( \frac{1}{1 \cdot 3}+\frac{1}{2 \cdot 4}+\frac{1}{3 \cdot 5}+\ldots+\frac{1}{n \cdot(n+2)}=\frac{n \cdot(3 \cdot n+5)}{4 \cdot(n+1) \cdot(n+2)} \)

Problem/Ansatz:

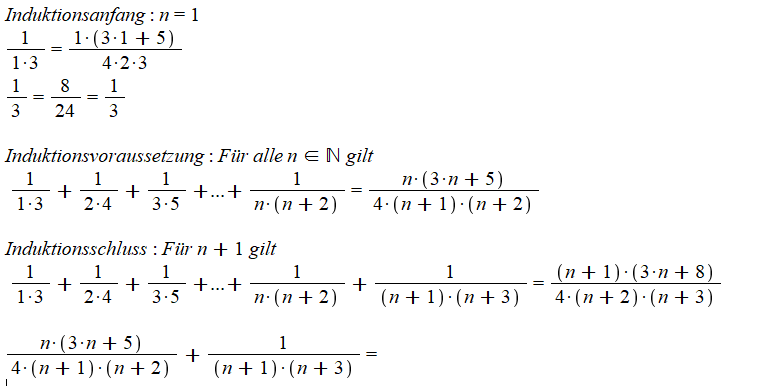
Text erkannt:

Induktionsanfang: \( n=1 \) \( \frac{1}{1 \cdot 3}=\frac{1 \cdot(3 \cdot 1+5)}{4 \cdot 2 \cdot 3} \)
\( \frac{1}{3}=\frac{8}{24}=\frac{1}{3} \)
Induktionsvoraussetzung : Für alle \( n \in \mathbb{N} \) gilt \( \frac{1}{1 \cdot 3}+\frac{1}{2 \cdot 4}+\frac{1}{3 \cdot 5}+\ldots+\frac{1}{n \cdot(n+2)}=\frac{n \cdot(3 \cdot n+5)}{4 \cdot(n+1) \cdot(n+2)} \)
Induktionsschluss : Für \( n+1 \) gilt \( \frac{1}{1 \cdot 3}+\frac{1}{2 \cdot 4}+\frac{1}{3 \cdot 5}+\ldots+\frac{1}{n \cdot(n+2)}+\frac{1}{(n+1) \cdot(n+3)}=\frac{(n+1) \cdot(3 \cdot n+8)}{4 \cdot(n+2) \cdot(n+3)} \)
\( \frac{n \cdot(3 \cdot n+5)}{4 \cdot(n+1) \cdot(n+2)}+\frac{1}{(n+1) \cdot(n+3)}= \)

Hallo ich komme bei dieser Aufgabe zur Vollständigen Induktion irgendwie nicht weiter.
Auh wenn ich die Brüche zusammenfasse, komme ich nicht auf die Lösung.

Gruß Jan

Answer 1

Hallo

erweitere das gesuchte Ergebnis mit (n+1)

und vergleiche dann mit dem Ergebnis der Addition  der 2 Brüche die du auf dein Hauptnenner gebracht hast.

oder mach Pölynomdivision durch (n+1)

lul