Text erkannt:
Satz \( 2.12 \) Ist die Funktion \( f: I \rightarrow \mathbb{R}(n+1)-m a l \) differenzierbar in \( I \), so gilt
$$ f(x)-T_{n}(x ; \widehat{x})=\frac{1}{(n+1) !} f^{(n+1)}(t)(x-\widehat{x})^{n+1} $$
wobei t eine (i.A. unbekannte) Zwischenstelle zwischen \( x \) und \( \widehat{x} \) bezeichnet.
Wir verzichten im weiteren auf einen Beweis dieses Satzes, veranschaulichen aber zumindest einmal seine Aussage im einfachsten Fall, nämlich für \( n=0 . \) In diesem Fall ist das Taylorpolynom die konstante Funktion \( T_{0}(x ; \widehat{x})=f(\widehat{x}) \) und eine einfache Umstellung der Gleichung des Satzes ergibt
$$ \frac{f(x)-f(\widehat{x})}{x-\widehat{x}}=f^{\prime}(t) $$
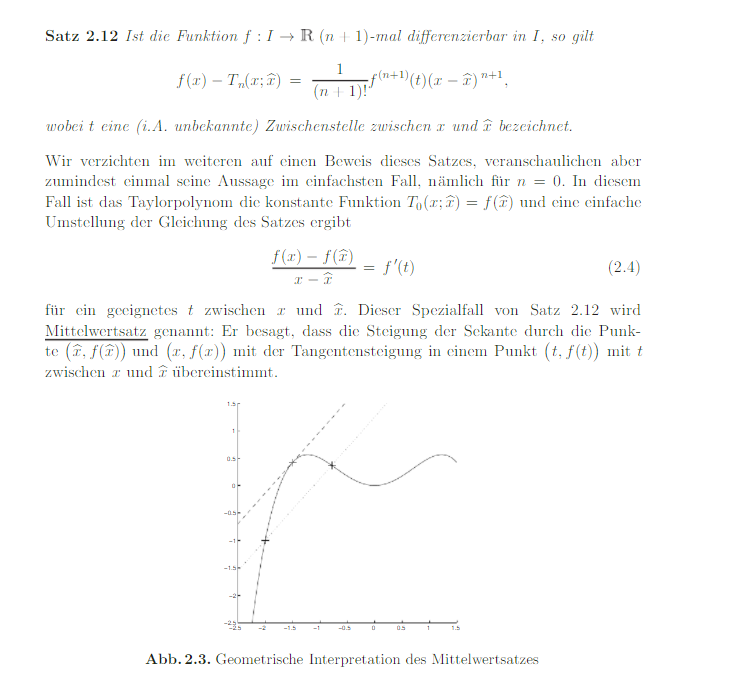
für ein geeignetes \( t \) zwischen \( x \) und \( \widehat{x} \). Dieser Spezialfall von Satz \( 2.12 \) wird Mittelwertsatz genannt: Er besagt, dass die Steigung der Sekante durch die Punkte \( (\widehat{x}, f(\widehat{x})) \) und \( (x, f(x)) \) mit der Tangentensteigung in einem Punkt \( (t, f(t)) \) mit \( t \) zwischen \( x \) und \( \widehat{x} \) übereinstimmt.
Abb. 2.3. Geometrische Interpretation des Mittelwertsatzes
das hier aber ich konnte damit wirklich 0 anfangen..