Berechnung unterschiedlicher Kreise im Umkreis, es sind aber nur Durchmesserverhältnisse der beiden gr. bekannt

Question

Aufgabe:

Wie berechnet man die unterschiedlich großen Kreise in einem Umkreis, wenn von den beiden größten nur das Durchmesserverhältnis zueinander bekannt ist?

Problem/Ansatz:

Bekannt sind die Größenverhältnisse (r1/r2) von zwei der inneren drei Kreise und der Radius (r0) des Umkreises.
(r2 und r3 können auch gleich groß sein)
Es sollen die Radien aller drei inneren Kreise (gelb) berechnet werden, die Radien der Randkreise (hellblau) sowie der Radius des inneren (grünen) Kreises.

Comments

Vom Duplikat:

Titel: Berechnung unterschiedlich großer Kreise (2+2) in einem Umkreis aber nur Durchmesserverhältnis ist bekannt

Stichworte: umkreis

Aufgabe:

Wie berechnet man die unterschiedlich großen Kreise in einem Umkreis, wenn von den beiden großen Paaren nur das Durchmesserverhältnis zueinander bekannt ist?



Problem/Ansatz:

Bekannt sind die Größenverhältnisse (r1/r2) von den inneren drei Kreise (siehe Bild) und der Radius (r0) des Umkreises.
Zwei Kreise nebeneinander haben den selben Radius (r1) und zwei weitere Kreise haben den selben Radius (r2).

(r1 und r2 sind die größten Radien von allen Kreisen innerhalb des Umkreises)
Es sollen die Radien aller vier inneren Kreise (gelb) berechnet werden sowie der Radius des inneren (grünen) Kreises.

Text erkannt:

\( =\left(\frac{13+1}{A}\right) \)

Die hellblauen Kreise brauchen nicht berechnet werden.

---

Wer auch immer diese Markierungen gesetzt hat sollte sich die beiden Fragen doch wenigstens mal ansehen.

Es ist nicht einmal erforderlich, lesen zu können; ein Blick auf die bunten Bildchen reicht.

Answer 1

Hallo,

eine sehr interessante Aufgabe. Man kann sie u.a. dadurch lösen, indem man einen weiteren Kreis \(k_s\) hinzufügt, dessen Mittelpunkt \(S\) im Berührpunkt von \(k_0\) (Umkreis) und \(k_1\) liegt. Der Radius von \(k_s\) ist \(r_s=2r_1\). Anschließend invertiert man die anderen Kreise an \(k_s\).

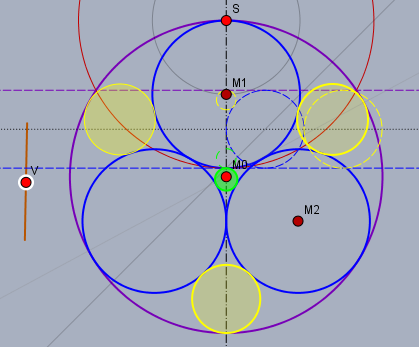
Diese Lage von \(k_s\) (rot) führt dazu, dass \(k_0\) (lila) und \(k_1\) (blau mit Mittelpunkt \(M_1\)) als Geraden abgebildet werden. Die Bilder der weiteren Kreise \(k_2\), \(k_3\) und die oberen der gelben Kreise, die sowohl \(k_0\) als auch \(k_1\) berühren, haben dann alle den gleichen Durchmesser, nämlich den Abstand \(d\) der beiden gestrichelten Parallelen.

Die Bilder des kleinen grünen Kreises und des unteren gelben Kreises haben einen Durchmesser von einem Viertel des Abstands \((d/4)\) der Parallelen. Sind die Bilder der Kreise bekannt, kommt man durch Spiegelung an \(k_s\) zu den Orginalen und ihren Radien.

Anbei nochmal zwei Szenarien mit unterschiedlichen Werten für das Verhältnis von \(r_1/r_2\)

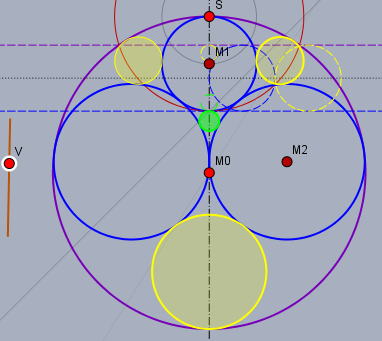
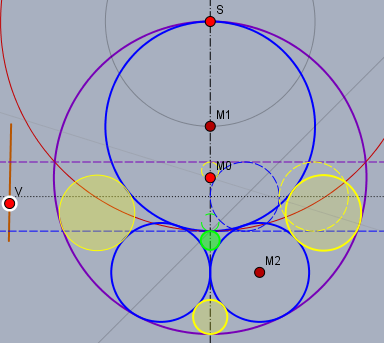
konstruieren (mit Zirkel und Lineal) kann ich es, aber ausrechnen ist ziemlich mühselig ;-)

Gruß Werner