Aufgabe:
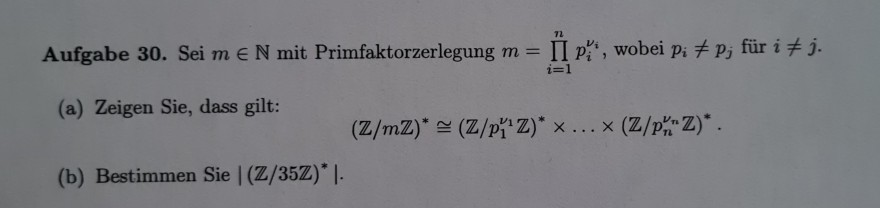
Text erkannt:
Aufgabe 30. Sei \( m \in \mathbb{N} \) mit Primfaktorzerlegung \( m=\prod \limits_{i=1}^{n} p_{i}^{\nu_{i}} \), wobei \( p_{i} \neq p_{j} \) für \( i \neq j \)
(a) Zeigen Sie, dass gilt:
\( (\mathbb{Z} / m \mathbb{Z})^{*} \cong\left(\mathbb{Z} / p_{1}^{\nu_{1}} \mathbb{Z}\right)^{*} \times \ldots \times\left(\mathbb{Z} / p_{n}^{\nu_{n}} \mathbb{Z}\right)^{*} \)
(b) Bestimmen Sie \( \left|(\mathbb{Z} / 35 \mathbb{Z})^{*}\right| \).
Siehe Bild
Problem/Ansatz:
Bei der a fehlt mir leider jeglicher Ansatz