Begründen Sie, warum Abbildung 1 und Abbildung 2 nicht die Wahrscheinlichkeitsverteilung von X darstellen.

Question

Aufgabe:

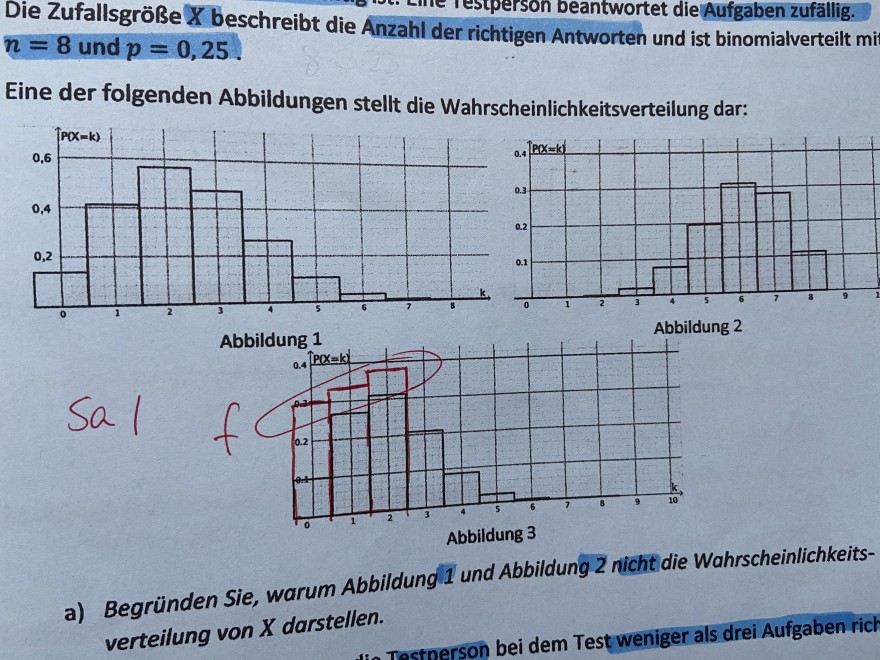
Beim Multiple Choice Test mit 8 Aufgaben gibt es je vier Antwortmöglichkeiten, bei denen jeweils eine Antwort richtig ist. Eine Testperson beantwortet die Aufgaben zufällig. Die Zufallsgröße X beschreibt die Anzahl der richtigen Antworten und ist binomialverteilt

n = 8 und p = 0,25

Eine der folgenden Abbildungen stellt die Wahrscheinlichkeitsverteilung dar:

A) Begründen Sie, warum Abbildung 1 und 2 nicht die Wahrscheinlichkeitsverteilung von X darstellen.

B) Das Ereignis A beschreibt, dass die Testperson bei dem Test weniger als 3 Aufgaben richtig beantwortet.

Problem/Ansatz:

Leider komme ich hier, trotz Erwartungswertberechnung nicht weiter.

Comments

Bei B. fehlt übrigens noch die Frage...

---

Vielen Dank :)) bei der B muss man dieses Ereignis in Abbildung 1 einzeichnen.

---

Eher in Abb. 3, nehme ich an?

---

Ja genau :))

---

Dann male halt die ersten drei Säulen (von links) bunt an.

Answer 1

A.

\( \left(\begin{array}{l}8 \\ k\end{array}\right) \cdot 0,25^{k}\cdot(1-0,25)^{8-k} \)

gibt für

k = 0 etwa 10 %

k = 2 etwa 31 %

B.

Die Summe für k = 0, 1 und 2 ist etwa 68 %

Answer 2

A) Begründen Sie, warum Abbildung 1 und 2 nicht die Wahrscheinlichkeitsverteilung von X darstellen.

Abbildung 1 zeigt gar keine Wahrscheinlichkeitsverteilung, da \(\sum \limits_{k=0}^{8} \left(X=k\right)\) offensichtlich größer als 1 ist.

Der Erwartungswert der Verteilung in Abbildung 2 ist offensichtlich nicht mit dem Erwartungswert \(n\cdot p=2\) von X identisch und zeigt daher auch nicht die Wahrscheinlichkeitsverteilung von X.