Aufgabe: Wir betrachten den Raum W mit der Testfunktion w(x), 0 < x < 6, die die Randbedinungen w(0) = 0 und w(6) = 0 erfüllt und beliebig oft differenzierbar ist.
Geben Sie ein Funktional S[T] so an, dass aus folgender Gleichung
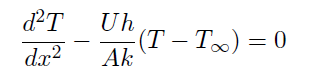
Text erkannt:
\( \frac{d^{2} T}{d x^{2}}-\frac{U h}{A k}\left(T-T_{\infty}\right)=0 \)
Euler-Lagrange-Gleichung wird, wenn man T mit w variiert.
(U, h, A, k und T∞ sind dabei Konstant, T definiert sich als eine Temperaturformel mit den Parametern x für die Position und t für die Zeit, mehr ist dazu nicht bekannt)
Problem/Ansatz:
Welchen Ansatz soll ich hier verfolgen?
Tendenziell würde ich das Gesamtenergie Funktional verwenden, ich weiss nur leider nicht wie ich das anwenden soll.
Gesamtenergie Funktional aus meinem Skript:
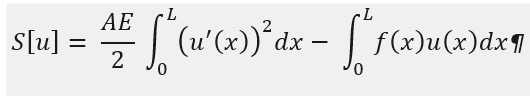
Vielen Dank für die Hilfe
Gruss SKP
Text erkannt:
\( S[u]=\frac{A E}{2} \int \limits_{0}^{L}\left(u^{\prime}(x)\right)^{2} d x-\int \limits_{0}^{L} f(x) u(x) d x \boldsymbol{\eta} \)