Sind die Geraden g und h parallel zueinander?

Question

Aufgabe:

Sind die Geraden g und h parallel zueinander?

g=AB mit A = (0 | -2), B = (3 | 0),

h=CD mit C = (0 | -2), D= (6 | 2)

Answer 1

Die Geraden haben mindestens den Punkt A=C gemeinsam. Da außerdem die Steigungen gleich sind, sind die Geraden identisch.

:-)

Comments

und rechnerisch?

---

m=Δy/Δx

m1=(0-(-2))/(3-0)=2/3

m2=(2-(-2))/(6-0)=4/6=2/3

:-)

---

@NichtMatheProfi:

mache Dir bei sowas immer eine Skizze

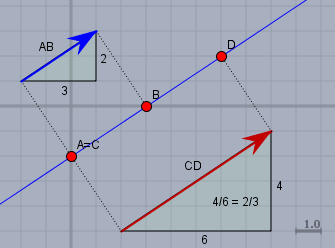
Beide Geraden haben einen gemeinsamen Punnkt \(A=C\). Und beide Richtungspfeile \(\vec{AB}\) (blau) und \(\vec{CD}\) (rot) weisen in die gleiche Richtung. Dies sieht man daran, dass das Verhältnis von vertikaler zu horizontaler Koordinate identisch ist \(2/3=4/6\).

Also sind die beiden Geraden identisch.

---

Es hat sich herausgestellt, dass ich nur die Vektoren ausrechnen hätte müssen und ein gemeinsames Vielfaches hinschreiben soll. Vielen Dank für Ihre Mühe!

---

Hallo,

es ist sinnvoll, wenn du in Zukunft schreibst, welches Thema ihr gerade behandelt. Die Aufgabe lässt sich ja auch ohne Vektoren lösen.

:-)