Hallo,
Zeichne ein Koordinatensystem ein, so dass die X-Achse durch \(OC\) verläuft. Dann kann man die Koordinaten der Punkte \(M\) und \(N\) in diesem System direkt berechnen.
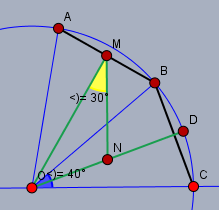
Es ist, mit Annahme dass der Radius \(|OC|=1\) ist$$N\left( \frac 12 \cos(20°),\, \frac 12 \sin(20°)\right)\\ M\left( |OM|\cos(60°),\, |OM|\sin(60°)\right) \\ |OM| = \cos(20°) $$Dann gibt es da den Zusammenhang Winkel \(\angle (a,b)\) und Skalarprodukt \(\left<a,\,b\right>\)$$\cos \left(\angle OMN\right) = \frac{\left< \vec{MO},\, \vec{MN}\right>}{|\vec{MO}|\cdot |\vec{MN}|} $$Mit dem Einsetzen der Größen wird es erst kryptisch, aber dann gleich viel einfacher, da die X-Koordinate von \(\vec{MN}\) gleich 0 ist.$$\cos \left(\angle OMN\right)= \frac{\left<\begin{pmatrix} -|OM|\cos(60°)\\- |OM|\sin(60°)\end{pmatrix},\, \begin{pmatrix} \frac 12 \cos(20°) - |OM|\cos(60°)\\\frac 12 \sin(20°) - |OM|\sin(60°) \end{pmatrix}\right>}{\cos(20°) \cdot \sqrt{\left( \frac 12 \cos(20°) - |OM|\cos(60°)\right)^2 + \left( \frac 12 \sin(20°) - |OM|\sin(60°)\right)^2}}\\\phantom{\cos \left(\angle OMN\right)}=\frac{- |OM|\sin(60°) \cdot \left(\frac 12 \sin(20°) - |OM|\sin(60°)\right)}{\cos(20°) \cdot\left| \frac 12 \sin(20°) - |OM|\sin(60°)\right|}\\\phantom{\cos \left(\angle OMN\right)}= \sin(60°) $$Mit \(\cos(\alpha) = \sin(90°-\alpha)\) folgt dann unmittelbar $$\angle OMN = 30°$$Gruß Werner