DAufgabe: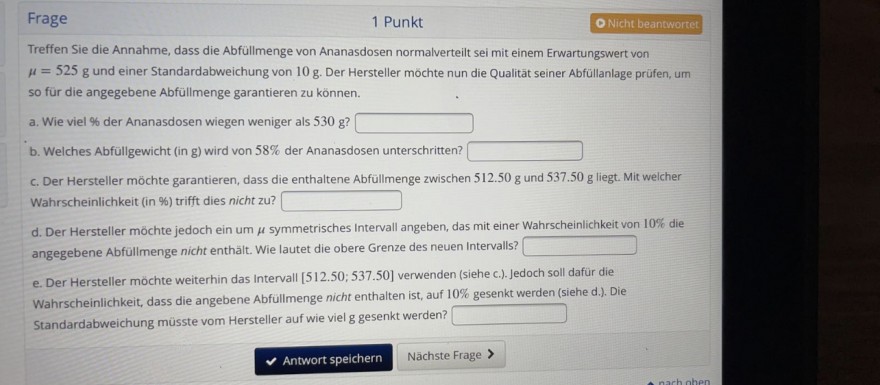
Text erkannt:
Frage \( \quad 1 \) Punkt
Treffen Sie die Annahme, dass die Abfullmenge von Ananasdosen normalverteilt sei mit einem Erwartungswert von \( \mu=525 \mathrm{~g} \) und einer Standardabweichung von \( 10 \mathrm{~g} \). Der Hersteller mochte nun die Qualităt seiner Abfüllanlage prüfen, um so für die angegebene Abfüllmenge garantieren zu können.
a. Wie viel \% der Ananasdosen wiegen weniger als \( 530 \mathrm{~g} \) ?
b. Welches Abfüligewicht (in g) wird von \( 58 \% \) der Ananasdosen unterschritten?
c. Der Hersteller möchte garantieren, dass die enthaltene Abfüllmenge zwischen \( 512.50 \mathrm{~g} \) und \( 537.50 \mathrm{~g} \) liegt. Mit welcher Wahrscheinlichkeit (in \%) trifft dies nicht zu?
d. Der Hersteller mochte jedoch ein um \( \mu \) symmetrisches Intervall angeben, das mit einer Wahrscheinlichkeit von \( 10 \% \) die angegebene Abfullmenge nicht enthält. Wie lautet die obere Grenze des neuen Intervalls? I?
e. Der Hersteller mochte weiterhin das Intervall \( [512.50 ; 537.50] \) verwenden (siehe c.). Jedoch soll dafür die Wahrscheinlichkeit, dass die angebene Abfullmenge nicht enthalten ist, auf \( 10 \% \) gesenkt werden (siehe d.). Die Standardabweichung müsste vom Hersteller auf wie viel g gesenkt werden?
vachste Frage
3
Kann mir bitte jemand sagen welches ich hier falsch habe bitte bin schon seit stunden dran.
a)69.1
b)527.01
c)21.13
d)523.74
e) 99.44
…
Problem/Ansatz: