DGL 2. Ordnung - Lösung einer inhomogenen Gleichung - partikuläre Lösung
DGL: y''+8y'+16y=e-4x
Mein Ansatz:
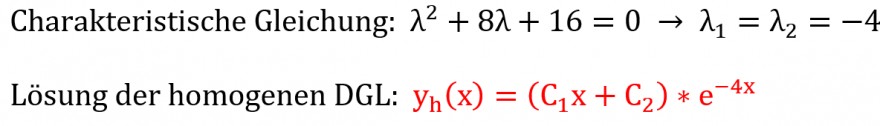
Text erkannt:
Charakteristische Gleichung: \( \lambda^{2}+8 \lambda+16=0 \rightarrow \lambda_{1}=\lambda_{2}=-4 \)
Lösung der homogenen DGL: \( \mathrm{y}_{\mathrm{h}}(\mathrm{x})=\left(\mathrm{C}_{1} \mathrm{x}+\mathrm{C}_{2}\right) * \mathrm{e}^{-4 \mathrm{x}} \)
Nächster Schritt wäre die partikuläre Lösung: y= yh + yp
yp=A*e-4x y'p= -4A*e-4x , y"= -16A*e-4x
Die Lösung meines Dozenten ist jedoch folgende:
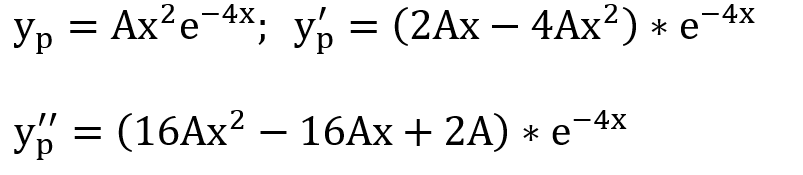
Text erkannt:
\( y_{p}=A x^{2} e^{-4 x} ; y_{p}^{\prime}=\left(2 A x-4 A x^{2}\right) * e^{-4 x} \)
\( y_{p}^{\prime \prime}=\left(16 A x^{2}-16 A x+2 A\right) * e^{-4 x} \)
Wie ist er auf das x2 gekommen? Die Störfunktion der DGL ist doch lediglich e-4x und nicht x2 * e-4x ??
Oder hat er sich da vertan? Was ist der richtige Ansatz für die partikuläre Lösung? bin da verwirrt
danke