Integral Aufgabe lässt mich verzweifeln

Question

Hallo Leute,

ich habe da ein Problem mit der folgenden Aufgabenstellung. An sich wie ich die Nullstellen, etc. berechne weiß ich, allerdings kann ich einfach dieses Integral nicht lösen. Weder per Substitution noch nach der partiellen Integration.

Integrationsrechner scheitern ebenfalls an der Aufgabe, weswegen ich stark vermute, dass man das Integral vlt. stark vereinfachen kann oder ähnliches? Sehe dies aber leider nicht.

Aufgabe:

f : [1,∞[ → ℜ : x ↦ \(\int\limits_{1}^{x}\\(\frac{e^{-t^{3}}}{2-cos(t)^{2}}·t dt \))

a) Bestimmen Sie alle Nullstellen von f.
b) Welche relativen und welche absoluten Extremwerte hat f auf [1,∞[ ?

Eine Nullstelle müsste ja x = 1 sein, da ja egal welche Stammfunktion hier herauskommt, die Subtraktion von
Oberergrenze - Unterergrenze = 0 ist.

Aber ich müsste ja beweisen, dass diese Nullstelle die einzige ist, falls keine weiteren existieren. Außerdem brauche ich für Aufgabe b eh die Stammfunktion, welche x enthält um diese für die Extremwerte abzuleiten.

Ich hoffe sehr ihr könnt mir hier weiterhelfen, weil mir sind die Ideen ausgegangen.

Comments

Du brauchst für dies Aufgabe die Stammfunktion nicht.

Überlege dir das mal so. Das Integral \( \int_0^x ... \) beschreibt ja die Fläche die der Integrand im Intervall \( [0,x] \) mit der x-Achse einschließt. Flächen oberhalb zählen positiv, Flächen unterhalb negativ. Jetzt lass dir mal den Integrand plotten. Was fällt dir auf?

Eine Nullstelle müsste ja x = 1 sein, da ja egal welche Stammfunktion hier herauskommt, die Subtraktion von
Oberergrenze - Unterergrenze = 0 ist.

Warum sollte hier Null rauskommen? Lass dir z.B. von WolframAlpha das Gegenteil bestätigen:

https://www.wolframalpha.com/input/?i=int_0%5E1+exp%28-t%5E3%29%2F%282-cos%28t%29%5E2%29+*+t+dt

---

kurz vorweg. ich hatte das integral falsch aufgeschrieben. die untere grenze ist 1 nicht null

---

Dann ist die Feststellung mit der Nullstelle bei x=1 natürlich richtig :) Am Rest der Aufgabe ändert das aber eigentlich nichts.

---

Schon mal danke für die Antwort und dafür dass du für ein besseres Verständnis meinerseits gesorgt hast. Das mit der Flächenbetrachtung hab ich schlecht weg vergessen.

ich hab das Ding jetzt mal geplottet. im Intervall [0,∞[ existiert ein schöner Hochpunkt bei ca. 0.6, der sich allerdings nicht im Definitionsbereich der Funktion f befindet [1,∞[.

Dh. da das Integral eine Flächenberechnung ist, ist dieser Wert für x = 1 am höchsten und geht dann immer weiter auf die Null zu.

Da die Funktion f(t) ab ca. t = 4 gleich Null entspricht und auch Null bleibt bei steigendem t, müsste dies ja bedeuteten, dass die Fläche ebenfalls Null ist und somit für f(x) unendlich viele Nullstellen existieren. Oder?

---

Wozu benötigst du die Stammfunktion?

---

Du verwechselst vermutlich den Integranden mit dem Integral

Blau der Integrand und orange ist (ungefähr) dein f

Da der Integrand positiv ist wird die Fläche zwischen x-Achse und Integrand mit wachsendem x doch größer oder?
Also ist die Integralfunktion monoton steigend, wie du auch oben im Bild siehst.Überall monoton steigende Funktionen haben keine lokalen Extrema. Bleiben globale Extrema am Rand, hier gibt es aber auch nur einen.

Answer 1

$$ f:\: \left[1,∞\right[ \rightarrow \mathbb{R},\quad x \mapsto \int\limits_{1}^{x}\left(\dfrac{\textrm{e}^{-t^{3}}}{2-\cos(t)^{2}}\cdot t\right) \textrm{ d}t $$ a) Bestimmen Sie alle Nullstellen von f.
b) Welche relativen und welche absoluten Extremwerte hat f auf \(\left[1,∞\right[\)?

Es fällt auf, dass der Integrand ist auf dem gesamten Integrationsintervall positiv ist. Was sagt uns das?

Comments

Ich verstehe nun folgendes:
Mit diesem Integral berechne ich die Fläche zwischen dem Integranden f(t) und der x-Achse. Anhand der Oberen Grenze x, wird ja nur der zur Berechnung der Fläche benötigte Abschnitt definiert. Dh. wird x größer, so wird auch der ausgerechnete Flächeninhalt größer. Also für jedes x gibt es daher einen Wert und letzten Endes auch eine Funktion f(x), die diesen Werten entspricht.
Für jedes x.

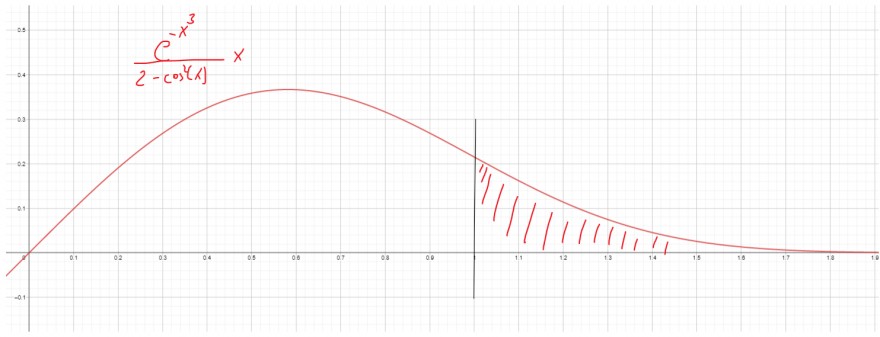
Nun kann ich ja simple zeigen, dass f(t) nur im positiven Wertebereich ist und für
t → ∞ gegen Null läuft  aber diese nie erreicht (außer für t = 0, aber das ist außerhalb des DB).
Dh. wiederum, dass die Funktion f(x) monoton steigend sein muss und wie bereits in meiner Fragestellung erwähnt nur die Nullstelle x = 1 besitzt.

Ich hab mal für x ein paar Werte ausgerechnet:

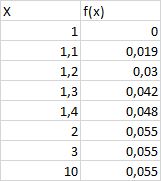
Text erkannt:

\begin{tabular}{|r|r|}
\hline \multicolumn{1}{|l|} {\( X \)} & \multicolumn{1}{l|} {\( f(x) \)} \\
\hline 1 & 0 \\
\hline 1,1 & 0,019 \\
\hline 1,2 & 0,03 \\
\hline 1,3 & 0,042 \\
\hline 1,4 & 0,048 \\
\hline 2 & 0,055 \\
\hline 3 & 0,055 \\
\hline 10 & 0,055 \\
\hline
\end{tabular}

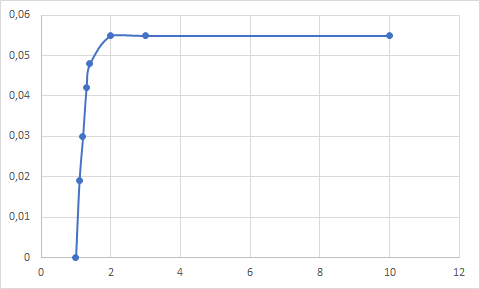
Demnach und mit der Erklärung, dass f(x) monoton steigend ist (f(t) geht sehr "schnell" gegen Null weswegen die Fläche nur sehr sehr wenig steigt), bedeutet dies ja, dass f(x) weder absolute noch relative Extremwerte besitzt.

Hab ich das soweit jetzt richtig verstanden? Sorry für die lange ausführliche Antwort, aber ich will auf Nummer sicher gehen, dass ich es verstanden habe.

---

Dh. wiederum, dass die Funktion f(x) monoton steigend sein muss

Genau. Und daher

bedeutet dies ja, dass f(x) weder absolute noch relative Extremwerte besitzt.

Na ja, jedenfalls besitzt f im Inneren ihres Definitionsbereiches keine Extremstellen. Bleibt als letzte Möglichkeit noch ein Blick auf den Rand.

Answer 2

So sieht das aus:

Die Nullstelle liegt bei t=0, Die graue Fläche ist gesucht und kann durch Trapezflächen eingeschachtelt werden.

Die Stammfunktion findet mein CAS nicht.

Comments

Die Nullstelle liegt bei t=0

Die Nullstelle des Integranden ist nicht gesucht.