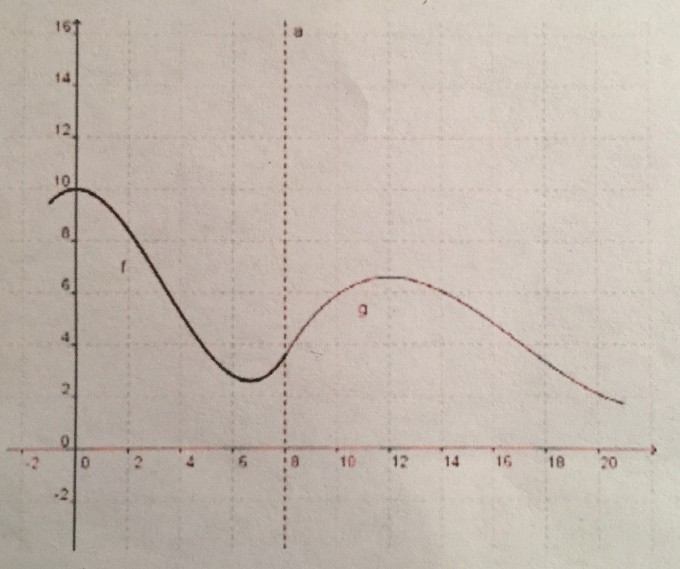
Eine Wasserrutsche ist in 2 Funktionsgraphen dritten Grades dargestellt.
Im Intervall (0;8) soll die Rutsche im höchsten Punkt auf einer Höhe von 10 Metern starten und nach 6 2/3 Metern seinen Tiefpunkt haben.
Beim Übergang zur Funktion g(x)=0,01(x-12)³-0,15(x-12)²+6,5 für den Intervall (8;21) hat die Rutsche die Steigung von 58°. Berechnen sie f(x) und geben sie das maximale Gefälle der Rutsche (von f(x) an.