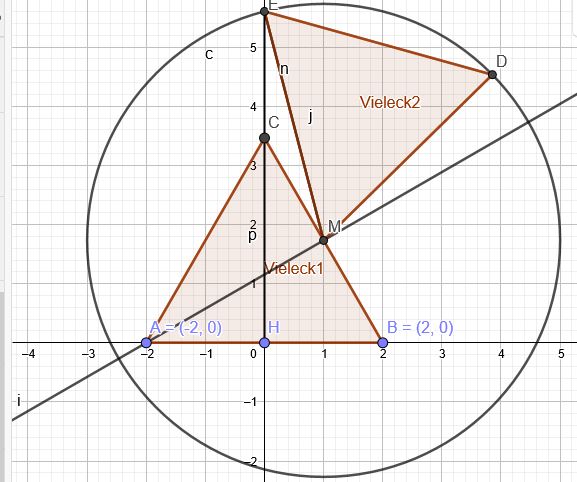
Grundlegend überarbeitet:
\(\overline{ME}=\overline{AB}\)
\(\overline{HC}=\frac{1}{2}\sqrt{3}\cdot \overline{AB}\)
Koordinaten von C:
\( \frac{y-0}{x+2}=\tan(60°) =\sqrt{3}\)
\( y=\sqrt{3}(x+2)\) An der Stelle \(x=0\):
\( y=2\sqrt{3}\)
C:\((0|2\sqrt{3})\)
Koordinaten von M: \((1|\sqrt{3})\)
Koordinaten von E:
Kreis um M: \((1|\sqrt{3})\) mit \(r=4\):
\((x-1)^2+(y-\sqrt{3})^2=16\) An der Stelle \(x=0\):
\(1+(y-\sqrt{3})^2=16\)
\((y-\sqrt{3})^2=15|±\sqrt{~~}\)
\(y-\sqrt{3}=\sqrt{15}\)
\(y=\sqrt{3}+\sqrt{15}\) Nötig ist nur der positive Wert.
Koordinaten von E:\((0|\sqrt{3}+\sqrt{15})\)
\(\overline{EH}=\sqrt{3}+\sqrt{15}\)
\(\overline{CH}=2\sqrt{3}\)
\( \frac{\overline{EH}}{\overline{CH}}=\frac{\sqrt{3}+\sqrt{15}}{2\sqrt{3}} \)