Der goldene Schnitt und das eng mit ihm verbundene Thema „Fibonaccizahlen“ haben einen engen Bezug zur belebten Natur, zur Kunst (einschließlich Baukunst), zu einigen (Brett-)Spielen und natürlich zur Geometrie sowie anderen Bereichen der Mathematik. Umso verwunderlicher ist es, dass das Thema „Goldener Schnitt“ im Mathematikunterricht eine geringe bis gar keine Rolle spielt. Dabei wird in der Didaktik die Suche nach motivierenden Inhalten eifrig thematisiert. Der goldene Schnitt hat insofern motivierenden Charakter, als er zahlreiche Querverbindungen innerhalb der Mathematik und auch zu Themen außerhalb der Mathematik ebenso sichtbar macht, wie die Schönheit der Mathematik. Was fehlt ist der Anwendungsbezug, wodurch das Thema in der heutigen didaktischen Lehrmeinung keinen Platz findet.
Der goldene Schnitt tritt in vielen geometrischen Aufgaben zu Tage, was an einigen Beispielen gezeigt wird, die zum Teil hier in der Mathelounge erschienen sind und trotz zahlreicher Aufrufe nicht beantwortet wurden. Statistik (Stand 27.06.2021; 16:30 Uhr):
Aufgabe Nr.
| Anzahl Aufrufe
| Anzahl Antworten
|
| 3 | 19 | 0 |
| 4 | 25 | 0 |
| 5 | 20 | 0 |
| 6 | 16 | 0 |
Liegt das Ausbleiben der Antworten vielleicht daran, dass derartige Aufgaben als schwierig angesehen werden oder vergleichbare Aufgaben unbekannt sind?
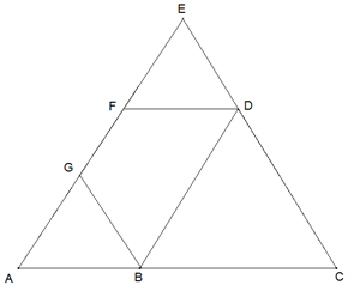
Aufgabe 1) Das gleichseitige Dreieck BCD habe die Seitenlänge 1. Wie lang muss die Seitenlänge des gleichseitigen Dreiecks ACE gewählt werden, damit BDFG und ACDF ähnliche Trapeze sind?
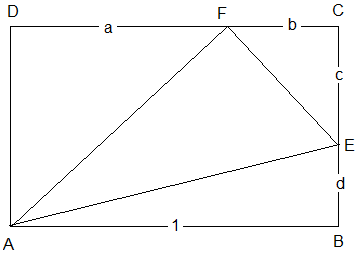
Aufgabe 2) Im Inneren eines Rechtecks ABCD mit |\( \overline{AB} \) |=1 liegt das Dreieck AEF mit E auf BC und F auf CD. Die übrigen Dreiecke im Inneren des Rechtecks seien flächengleich. In welchem Verhältnis teilt E die Strecke \( \overline{BC} \) bzw. teilt F die Strecke \( \overline{DC} \) ?
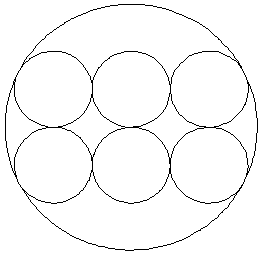
Aufgabe 3) Sechs Münzen liegen auf einem Bierdeckel (siehe Abbildung). In welchem Verhältnis stehen Bierdeckelradius und Münzdurchmesser?
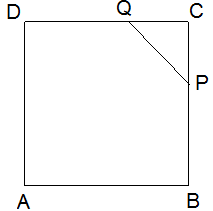
Aufgabe 4) Im Quadrat ABCD liegen P und Q auf den Quadratseiten CB bzw. DC und haben von C den gleichen Abstand. Die Flächen der Dreiecke ABP und APQ seien gleichgroß. In welchem Verhältnis teilen P bzw. Q die Quadratseiten, auf denen sie liegen?
Aufgabe 5) ABC sei ein gleichseitiges Dreieck mit den Mitten L und M zweier Seiten. Die Gerade LM schneidet den Umkreis von ABC insbesondere in N, sodass M auf (\( \overline{LN} \) ) liegt. Wie teilt M die Strecke (\( \overline{LN} \) ) ?
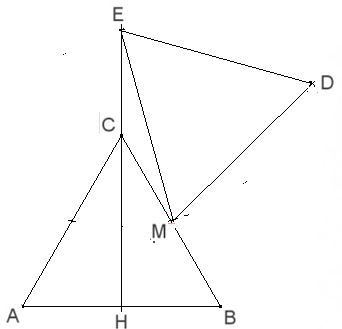
Aufgabe 6) ABC sei ein gleichseitiges Dreieck, H die Mitte von AB und M die Mitte von BC. E auf HC sei der Eckpunkt eines Dreiecks MDE, das zu ABC kongruent ist. Wie groß ist das Längenverhältnis |\( \overline{EH} \) |/|\( \overline{CH} \) | ?
.