Aufgabe:
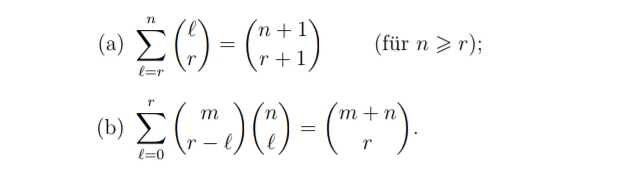
Text erkannt:
(a) \( \sum \limits_{\ell=r}^{n}\left(\begin{array}{l}\ell \\ r\end{array}\right)=\left(\begin{array}{l}n+1 \\ r+1\end{array}\right) \)
\( ( \) für \( n \geqslant r) \)
(b) \( \sum \limits_{\ell=0}^{r}\left(\begin{array}{c}m \\ r-\ell\end{array}\right)\left(\begin{array}{l}n \\ \ell\end{array}\right)=\left(\begin{array}{c}m+n \\ r\end{array}\right) \).
Problem/Ansatz:
Ich soll die obigen Identitäten beweisen. Bei a) weiß ich, dass ich das mit der vollständigen Induktion machen könnte. Leider scheitere ich schon beim Induktionsanfang. Wenn ich annehme, dass die Gleichung für n=0 gilt, weiß ich nicht, wie ich fortfahren soll...
Ich würde mich über jede Hilfe freuen!