Wolframalpha partielles Ableiten

Question

Aufgabe:

ich versuche gerade mithilfe Wolframalpha partiell abzuleiten. Das ganze klappt ganz gut, nur jetzt soll ich den natürlichen Logarythmus verwenden. Habe meiner Ansicht nichts falsch gemacht, klappt dennoch nicht...

Text erkannt:

Antwort
Bestimmen Sie die partielle Ableitung \( f_{1}^{\prime}\left(x_{1}, x_{2}\right) \) der Funktion
$$ f\left(x_{1}, x_{2}\right)=x_{1}^{6} \cdot \ln \left(\frac{x_{2}^{6}}{x_{1}^{6}+x_{2}^{6}}\right) $$
an der Stelle \( \mathbf{a}=\left(\begin{array}{l}1.16 \\ 1.07\end{array}\right) \).

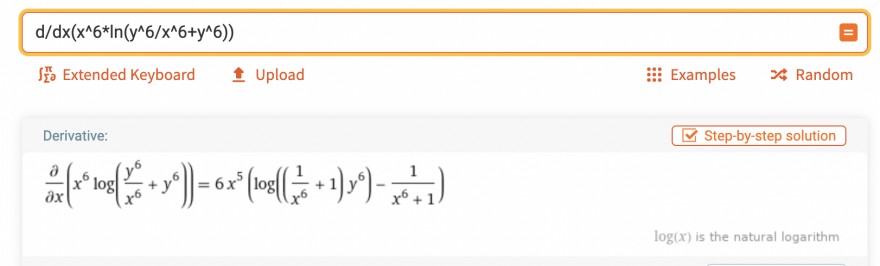
Text erkannt:

\( \mathrm{d} / \mathrm{dx}\left(\mathrm{x}^{\wedge} 6^{*} \ln \left(\mathrm{y}^{\wedge} 6 / \mathrm{x}^{\wedge} 6+\mathrm{y}^{\wedge} 6\right)\right) \)
Derivative:
\( \frac{\partial}{\partial x}\left(x^{6} \log \left(\frac{y^{6}}{x^{6}}+y^{6}\right)\right)=6 x^{5}\left(\log \left(\left(\frac{1}{x^{6}}+1\right) y^{6}\right)-\frac{1}{x^{6}+1}\right) \)
the \( \mathrm{m} \)

Ergebnis ist aber falsch... vll sieht jemand meinen Fehler :D

Comments

Du hast die Nennerklammer vergessen!

Answer 1

Fällt dir nicht auf das Dein Term bei Wolframalpha eigentlich ganz anders aussieht?

So sollte das bei Wolframalpha aussehen

Comments

Habs mit deinem probiert, kommt -12,67 raus. Ergebnis ist aber -19,95.

---

Dann kannst du die Werte nicht mal in die Formel einsetzen :-(

6·1.16^5·(LN(1.07^6/(1.16^6 + 1.07^6)) - 1.16^6/(1.16^6 + 1.07^6)) = -19.95314436

Answer 2

Du hast den Nenner des Bruchs nicht in Klammern gesetzt.

Grüße,

Algebravo