Dreieck konstruieren (Hc, r und beta)

Question

Aufgabe:

Ich soll ein Dreieck klassisch konstruieren (mit Zirkel). Gegeben sind die Höhe= 8cm, Innenwinkel beta= 40 Grad und der Inkreisradius r= 2cm.

Problem/Ansatz:

Wie muss ich jetzt beginnen?

Comments

Gegeben sind die Höhe= 8cm

Welche der drei Höhen ist das ?

Answer 1

Hallo

Teildreieck aus Seite b, Winkel beta und h ist der Anfang, Winkelhalbierende von beta, darauf liegt Mittelpunkt  M des Umkreises, Parallele dazu durch B senkrechte vom Schnittpunkt  auf Wh gibt M, Rest sollte klar sein.

lul

Answer 2

Beginne mit den freien Schenkeln des Winkel β bei B. Konstruiere die Winkelhalbierende von β. Eine Parallele zu einem freien Schenkel von  β im Abstand r=3 schneidet die Winkelhalbierende von β. Nun Inkreis herstellen. Ich habe nun als Höhe h_c =9 gewählt. Den weiteren Weg erkennst du auf beigefügter Zeichnung.

Comments

Achtung! Bei mir beträgt der Inkreisradius 3cm statt 2 cm und die Höhe 9cm statt 8cm.

Answer 3

Eine alternative Konstruktion:

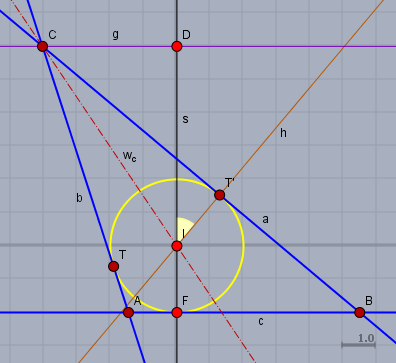
Zeichne den Inkreis \(k\) mit \(r=2\) und Mittelpunkt \(I\). Dann eine Gerade \(s\) (schwarz) durch \(I\), die \(k\) in \(F\) schneidet. Trage dann die Höhe \(h_c=8\) auf \(s\) ausgehend von \(F\) ab, so dass das andere Ende der Strecke (Punkt \(D\)) auf der gegenüberliegenden Seite von \(I\) liegt (s. Skizze). Zeiche den Winkel \(\beta=40°\) in \(I\). Der freie Schenkel \(h\) (braun) schneidet \(k\) in zwei Punkten. \(T'\) ist der Punkt, der \(D\) am nächsten liegt.

Konstruiere die Senkrechte \(g\) (lila) zu \(s\) durch \(D\), die Senkrechte \(a\) (blau) zu \(h\) durch \(T'\) und die Senkrechte \(c\) (blau) zu \(s\) durch \(F\). \(g\) und \(a\) schneiden sich im Punkt \(C\) und \(a\) und \(c\) schneiden sich im Punkt \(B\).

Zeichne nun die Gerade \(w_c\) (rot) durch die Punkte \(C\) und \(I\) und spiegele den Punkt \(T'\) an \(w_c\) zum Punkt \(T\). Die Gerade durch \(C\) und \(T\) ist \(b\). \(b\) schneidet \(c\) im Punkt \(A\).

\(\triangle ABC\) ist das gesuchte Dreieck.