Veranschaulichen komplexer Zahlen Kreis

Question

Wie erkenne ich, dass es sich bei folgender Teilmenge der komplexen Zahlen um einen Kreis um 1/2 mit Radius 1/2 ohne Null handelt?

$$Re(\frac{1}{z})=1, z \neq0$$

Nach Umformen komme ich auf:

$$\frac{x}{x^2+y^2}=1$$

Weiß jemand wie ich dann weitermachen soll?

Danke für die Hilfe.

Answer 1

Hallo Chris,

Du kannst die Gleichung mit \(x^2+y^2\) multiplizieren und dann noch etwas umformen$$\begin{aligned} \frac x{x^2+y^2} &= 1 &&|\, \cdot (x^2+y^2)\\ x &= x^2 + y^2 &&|\, -x\\ 0 &=x^2 - x + y^2\\ 0 &= x^2 - x + 0,5^2 + y^2 - 0,5^2&&|\, +0,5^2 \\ 0,5^2 &= (x-0,5)^2 + y^2\end{aligned}$$und so erhältst Du die Kreisgleichung für einen Kreis mit Mittelpunkt bei \((0,5|\, 0)\) und Radius \(0,5\).

Versuche Dir das mal an Hand der Geometrie zu veranschaulichen:

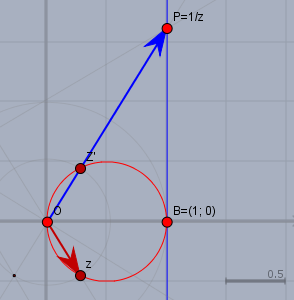
Der Realteil von \(1/z\) ist \(=1\) und damit liegt \(1/z\) auf der blauen Senkrechten. Invertiert man \(1/z\) zu \(z\), so kommt man zum roten Kreis.

Nach dem Sekanten-Tangenten-Satz ist$$\begin{aligned}|PO| \cdot |PZ'| &= |PB|^2 \\ |PO| \cdot(|PO| - |Z'O|) &= |PO|^2 - 1 \\ |PO|\cdot |Z'O| &= 1 \\ |Z'O| &= \frac1{|PO|}= \frac 1{\left|\frac 1z\right|} = |z|\end{aligned}$$Zusammen mIt \(\arg(1/z) =-\arg(z)\) kommt man dann genau bei \(z\) (roter Pfeil) heraus.

Gruß Werner

Comments

Antwort um die geometrische Anschauung erweitert.

---

was mir noch einfiel: Die Abildung \(z \to 1/z\) entspricht geometrisch einer Spiegelung am Einheitskreis (schwarz s.u.) verknüpft mit einer Spiegelung an der reellen Achse.

Folglich wird eine senkrechte Gerade durch den Punkt \(B(1|\,0)\) auf einen Kreis abgebildet, dessen Durchmesser die Strecke \(OB\) ist - und umgekehrt.

https://jsfiddle.net/WernerSalomon/5soakfq2/22/

Verschiebe den Punkt \(Z\) mit der Maus. Solange er sich auf dem roten Kreis befindet, ist seine Abbildung \(1/z\) auf der blauen Senkrechten.

Answer 2

Hallo,

\(\frac{x}{x^2+y^2}=1 \Leftrightarrow x^2+y^2-x=0\)

Du kannst auf den rechten Ausdruck nun die quadratische Ergänzung anwenden auf die \(x\)-Terme: \(x^2-x=\left(x-\frac{1}{2}\right)^2-\frac{1}{4}\).

Dann gilt:$$\left(x-\frac{1}{2}\right)^2+y^2=\frac{1}{4}$$ Also ein Kreis mit Mittelpunkt \(M(0.5|0)\) und Radius \(r=\frac{1}{2}\).

Answer 3

Kreis um 1/2 mit Radius 1/2

Der hat die Gleichung

        \(\left(x-\frac{1}{2}\right)^2 + y^2 = \frac{1}{4}\).

\(\frac{x}{x^2+y^2}=1\)

Forme um so dass du obige Glecihung bekommst.