Bestimmen Sie alle x \in \mathbb{R} , die die Ungleichung

Question

(a) Bestimmen Sie alle \( x \in \mathbb{R} \), die die Ungleichung
$$ \frac{3|x-2|}{3 x-2}<-2 $$
erfüllen.

Comments

Ich weiß, die aufgabe ist sehr schwer, kann mir trotzdem jemand helfen?

---

Ohne Ansatz etwas schwer zu helfen....

Answer 1

Der Nenner wechselt sein Vorzeichen bei x=2/3, der Term zwischen den Betragsstrichen bei x=2.

Du musst also 3 Fälle unterscheiden.

1) x<2/3

3x-2<0

x-2<0 → |x-2|=2-x

\(\frac{3|x-2|}{3 x-2}<-2 \)

3*(2-x) > -2*(3x-2)

6-3x > -6x+4

3x > -2

x> -2/3

--> -2/3 < x < +2/3

2) 2/3 < x < 2

3x-2>0

x-2<0 → |x-2|=2-x

\(\frac{3|x-2|}{3 x-2}<-2 \)

3*(2-x) < -2*(3x-2)

6-3x < -6x+4

3x < -2

x< -2/3 → Widerspruch zur Voraussetzung

3) x≥2

3x-2>0

x-2≥0 → |x-2|=x-2

\(\frac{3|x-2|}{3 x-2}<-2 \)

3*(x-2) < -2*(3x-2)

3x-6 < -6x+4

9x<10

x<10/9 → Widerspruch!

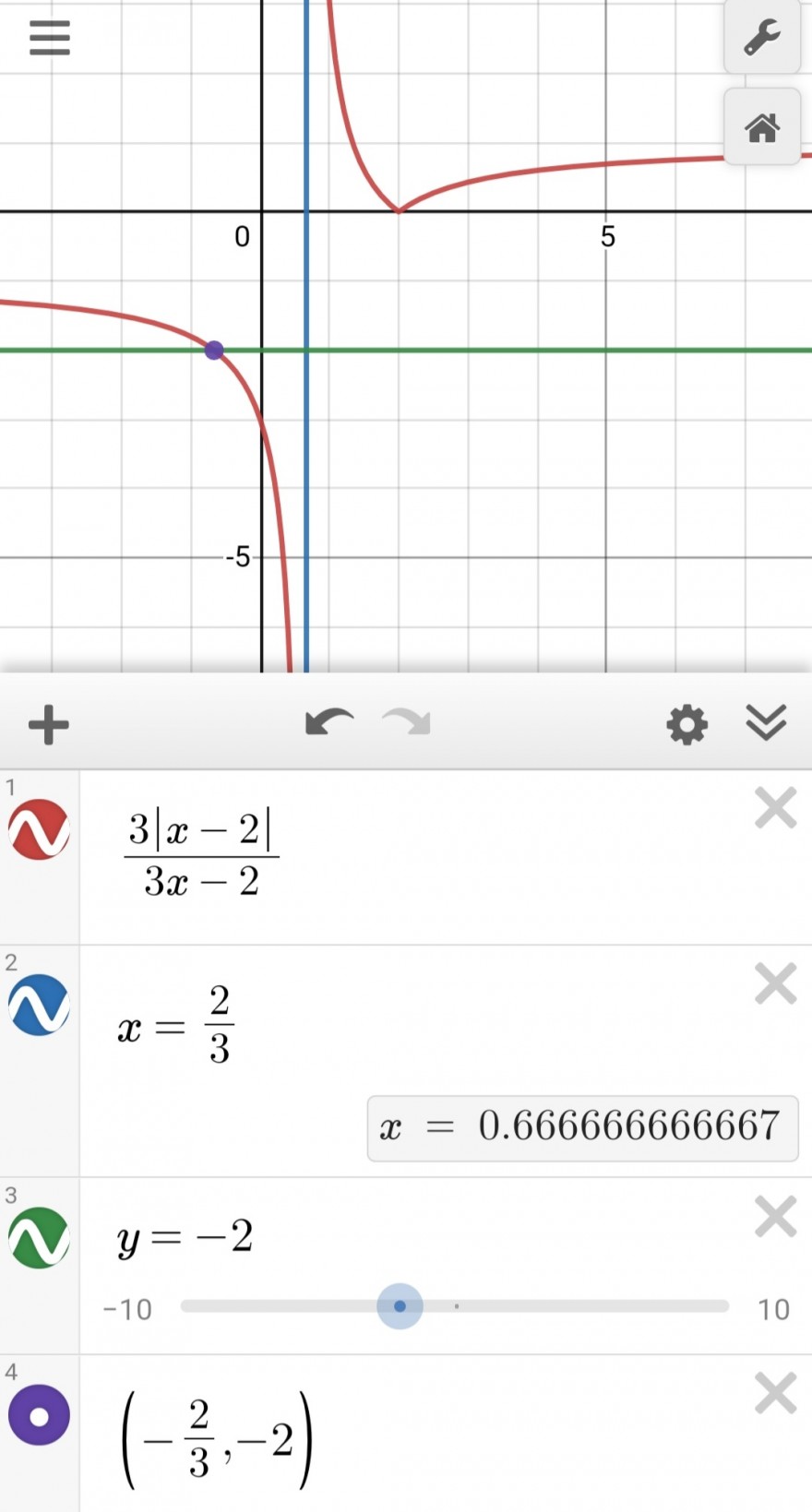
Ergebnis: -2/3 < x < +2/3

:-)

Comments

Danke erstmal. Würdest du hierbei noch helfen

Betrachten Sie die Folge \( \left(a_{n}\right) \) mit \( a_{n}=\frac{\sqrt{n}+1}{n^{3}} \). Beweisen Sie mit Hilfe der Definition des Grenzwerts, dass die Folge \( \left(a_{n}\right) \) den Grenzwert 0 besitzt.