Aufgabe:
b) Um Gebäude vor Blitzeinschlägen zu schützen, werden Blitzableiter verwendet. Dabei wird
eine Metallstange, die sogenannte Fangstange, auf dem Gebäude senkrecht montiert.
Der höchste Punkt einer solchen Fangstange kann als Spitze eines drehkegelförmigen
Schutzbereichs angesehen werden. Alle Objekte, die sich vollständig innerhalb dieses
Schutzbereichs befinden, sind vor direkten Blitzeinschlägen geschützt.
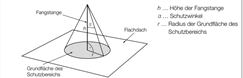
Text erkannt:
\( b \)
1) Erstellen Sie eine Formel zur Berechnung des Radius r aus α und h. r = h * tan(beta) was kein Problem war
Auf einem Flachdach ist eine 2 m hohe Fangstange senkrecht montiert. 3 m vom Fußpunkt der Fangstange entfernt steht eine 1,2 m hohe Antenne senkrecht auf dem Flachdach. Der Schutzwinkel beträgt 77°.
2) Überprüfen Sie nachweislich, ob sich diese Antenne vollständig innerhalb des Schutzbereichs befindet.
Problem/Ansatz:
nur 1. warum errechne ich dann 3/tan(beta) die 0,69 um dann weiter 2-0,69 die 1,30 zu errechnen?
und 2. aus welcher Formel kommt die r=h*tan(beta) denn ich finde es in der Formelsammlung nicht. Muss ich dass einfach wissen, oder kann ich das ableiten von irgendeiner Formel?
DANKE für Tipps
Teil der Formelsammlung, die man verwenden darf, ist:
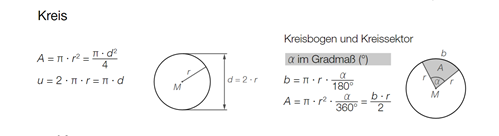
Text erkannt:
Kreis
\( A=\pi \cdot r^{2}=\frac{\pi \cdot d^{2}}{4} \)
\( u=2 \cdot \pi \cdot r=n \cdot d \)
Kreisbogen und Kreissektor
Text erkannt:
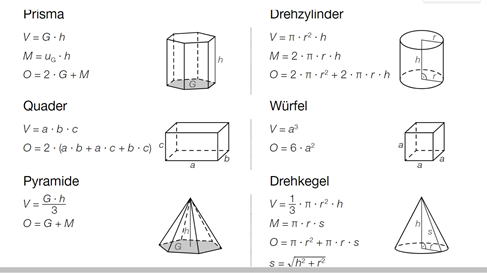
Prisma \( \quad \) Drehzylinder
\( V=G \cdot h \)
\( M=u_{G} \cdot h \)
\( O=2 \cdot G+M \)
\( \begin{array}{ll}\text { Quader } & \text { Würfel }\end{array} \) \( \begin{array}{l}V=a \cdot b \cdot c \\ O=2 \cdot(a \cdot b+a \cdot c+b \cdot c) c\left[\lambda-\ldots_{b}\right.\end{array} \mid \begin{array}{l}V=a^{3} \\ O=6 \cdot a^{2}\end{array} \)
Pyramide Drehkegel
\( V=\frac{G \cdot h}{3} \)
\( O=G+M \)
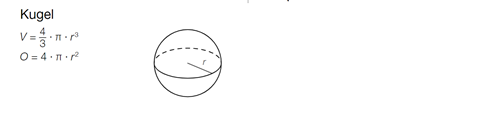
Text erkannt:
\( =\theta \)
Text erkannt:
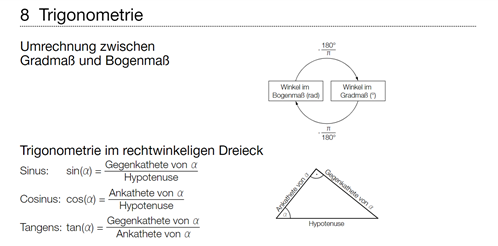
8 Trigonometrie
Umrechnung zwischen Gradmaß und Bogenmaß
Trigonometrie im rechtwinkeligen Dreieck Sinus: \( \sin (\alpha)=\frac{\text { Gegenkathete von } \alpha}{\text { Hypotenuse }} \)
Cosinus: \( \cos (\alpha)=\frac{\text { Ankathete von } \alpha}{\text { Hypotenuse }} \)
Tangens: \( \tan (\alpha)=\frac{\text { Gegenkathete von } \alpha}{\text { Ankathete von } \alpha} \)
Text erkannt:
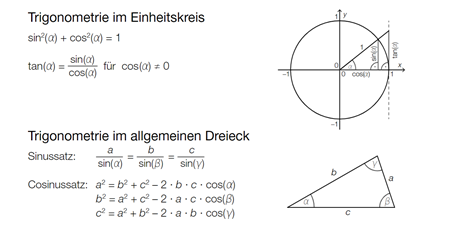
Trigonometrie im Einheitskreis \( \sin ^{2}(\alpha)+\cos ^{2}(\alpha)=1 \)
\( \tan (\alpha)=\frac{\sin (\alpha)}{\cos (\alpha)} \) für \( \cos (\alpha) \neq 0 \)
Trigonometrie im allgemeinen Dreieck Sinussatz: \( \quad \frac{a}{\sin (\alpha)}=\frac{b}{\sin (\beta)}=\frac{c}{\sin (y)} \)
Cosinussatz: \( a^{2}=b^{2}+c^{2}-2 \cdot b \cdot c \cdot \cos (\alpha) \)
\( b^{2}=a^{2}+c^{2}-2 \cdot a \cdot c \cdot \cos (\beta) \)
\( c^{2}=a^{2}+b^{2}-2 \cdot a \cdot b \cdot \cos (y) \)
Text erkannt:
Trigonometrische Flächenformel:
\( A=\frac{1}{2} \cdot b \cdot c \cdot \sin (\alpha)=\frac{1}{2} \cdot a \cdot c \cdot \sin (\beta)=\frac{1}{2} \cdot a \cdot b \cdot \sin (V) \)
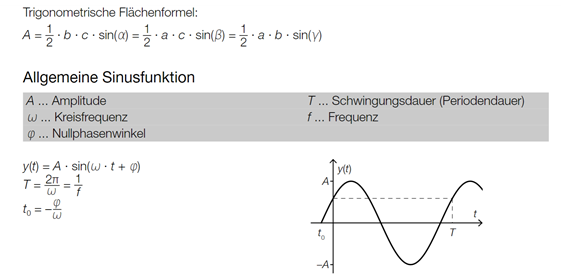
Allgemeine Sinusfunktion
\( A \)... Amplitude
\( T \ldots \) Schwingungsdauer (Periodendauer)
\( \omega \ldots \) Kreisfrequenz
\( f \ldots \) Frequenz
\( \varphi \ldots \) Nullphasenwinkel
\( y(t)=A \cdot \sin (\omega \cdot t+\varphi) \)
\( T=\frac{2 \pi}{\omega}=\frac{1}{f} \)
\( t_{0}=-\frac{\varphi}{\omega} \)
