Aufgabe:
Martin Modder interessiert sich dafür, wie viel seine Kunden für ihren Mobilfunkvertrag ausgeben – er überlegt nämlich, selbst in dieses Geschäft einzusteigen. Dazu hat er eine Kundenbefragung durchgeführt, in der 900 Befragte ihre monatlichen Kosten angegeben haben.
Der Mittelwert dieser Stichprobe beträgt 14,50 Euro, als Standardabweichung der Stichprobe lassen sich 9 Euro beobachten. Berechnen Sie, in welchem Intervall der tatsächliche Wert mit einer Wahrscheinlichkeit von 0,95 tatsächlich liegen dürfte.
Problem/Ansatz:
In dieser Aufgabe soll scheinbar das Konfidenzintervall ermittelt werden.
Die Parameter für die Funktion sind:
n = 900
Mittelwert = 14.5
Standardabweichung = 9
Alpha = 1-0.95 = 0.05
Berechnung
Die Formel für das Konfidenzintervall lautet: KI=[Mittelwert +- tn-1;1-(alpha/2*(s/Wurzel n)]
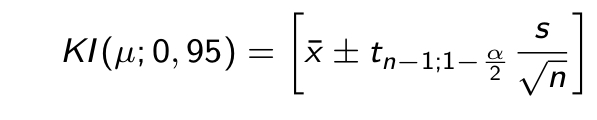
Da das n in der Aufgabe größer als 30 ist, muss ich auf die Tabelle der Normalverteilung zurückgreifen. Das Z für die Tabelle berechnet sich aus Z=(X-Erwartungswert)/Standardabweichung
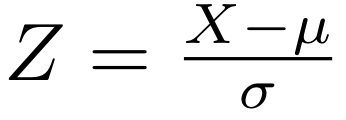
Allerdings weiß ich nicht recht, wie ich die Parameter X und μ festlege, um Z für die Tabelle der Normalverteilung zu berechnen.
.find_in_page{background-color:#ffff00 !important;padding:0px;margin:0px;overflow:visible !important;}.findysel{background-color:#ff9632 !important;padding:0px;margin:0px;overflow:visible !important;}
