Ist es richtig dass diese Funktion keine Extremstellen hat? 1/ (x+y)

Question

Aufgabe:

1/(x+y)

Problem/Ansatz:

Ist es richtig dass diese Funktion keine Extremstellen hat?

Answer 1

Hallo,

Ist es richtig dass diese Funktion keine Extremstellen hat? ->JA

Answer 2

Aloha :)

Willkommen in der Mathelounge... \o/

Bei einer Extremstelle muss der Gradient verschwinden:

$$\operatorname{grad}\left(\frac{1}{x+y}\right)=\binom{-\frac1{(x+y)^2}}{-\frac1{(x+y)^2}}\stackrel!=\binom{0}{0}$$Es gibt kein Koordinatenpaar \((x;y)\), das diese Forderung erfüllt:$$-\frac{1}{(x+y)^2}=0\quad\stackrel{\cdot(x+y)^2}{\implies}\quad-1=0\quad\text{Widerspruch}$$

Comments

@Mathenoob161: ohne irgendwas zu rechnen hilft es schon, wenn man sich ein Bild vom Verlauf der Funktion macht. Ist der Term \((x+y)\) konstant - und das ist er bei jeder Parallele zu \(y=-x\) - dann ist auch der Funktionswert konstant. Und senkrecht dazu - in Richtung von \(y=x\) - verhält sich die Funktion wie $$f(x) = \frac1{2x}$$

~plot~ 1/(2x) ~plot~

und diese Funktion ist durchweg monoton fallend, mit einem Pol bei \(x=0\). Sie kann also kein lokales Maximum oder Minimum haben.

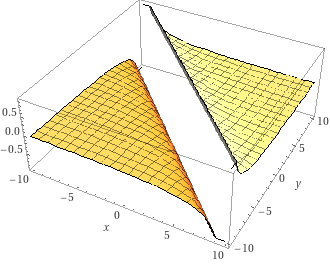
In 3D sieht die Funktion so aus: