Bestimme den Faktor k, wenn der Ball nach 20m auf dem Boden aufschlägt.

Question

Aufgabe:

Die Wurfhöhe y eines Balls hängt von der waagrechten Entfernung x von der Abwurfstelle ab und lässt sich durch die Funktion y(x)=k*x²+4*x beschreiben.

1) Bestimme den Faktor k, wenn der Ball nach 20m auf dem Boden aufschlägt.

2) In welcher Höhe befindet sich der Ball bei einer Entfernung von 5m?

3) In welcher Entfernung erreicht der Ball seine maximale Höhe und wie hoch ist diese?

4) Wie viele Meter ist der Ball bei einer Höhe von 8m von der Abwurfstelle entfernt?

Bitte alle Rechenschritte schreiben, sodass ich die Aufgabe gut verstehe.

Problem/Ansatz:

Ich verstehe die Aufgabe nicht,

Bitte Schrittweise schreiben, sodass ich sie endlich verstehe.

Comments

Tja, die Aufgabe ist etwas seltsam. Beim Abwurf ist der Ball 0 Meter waagerecht von der Abwurfstelle entfernt. Seine Höhe beträgt dann aber auch 0 Meter. Wird der Ball vom Boden aus "geworfen"? Sowas macht doch keiner.

Answer 1

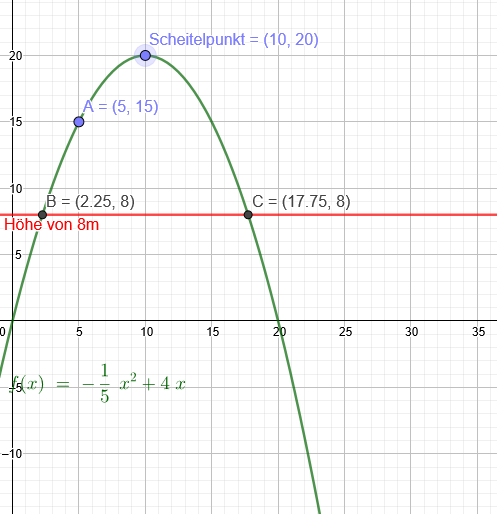
y(x)=k*x²+4*x

1) Bestimme den Faktor k, wenn der Ball nach 20m auf dem Boden aufschlägt.

y(20)=k*20²+4*20

400k+80=0     40k+8=0   k=-\( \frac{8}{40} \)=-\( \frac{1}{5} \)

y(x)=-\( \frac{1}{5} \)*x²+4*x

2) In welcher Höhe befindet sich der Ball bei einer Entfernung von 5m?

y(5)=-\( \frac{1}{5} \)*5²+4*5=-5+20=15

3) In welcher Entfernung erreicht der Ball seine maximale Höhe und wie hoch ist diese?

y´(x)=-\( \frac{1}{5} \)*2x+4

-\( \frac{1}{5} \)*2x+4=0

x=10    ( Schau dir mal die Zeichnung an, wie du auch an die x-Stelle der maximalen Höhe kommen kannst.)

y(10)=-\( \frac{1}{5} \)*10²+4*10=20

4) Wie viele Meter ist der Ball bei einer Höhe von 8m von der Abwurfstelle entfernt?

-\( \frac{1}{5} \)*x²+4*x=8|*(-5)

x^2-20x=-40

(x-10)^2=-40+10^2=60|\( \sqrt{} \)

1.) x-10=\( \sqrt{60} \)

x₁=10+\( \sqrt{60} \)≈17,75

2.) x-10=-\( \sqrt{60} \)

x₂=10-\( \sqrt{60} \)≈2,25