Aufgabe:
Text erkannt:
[0 Aufgabe \( 12.2 .6 \)
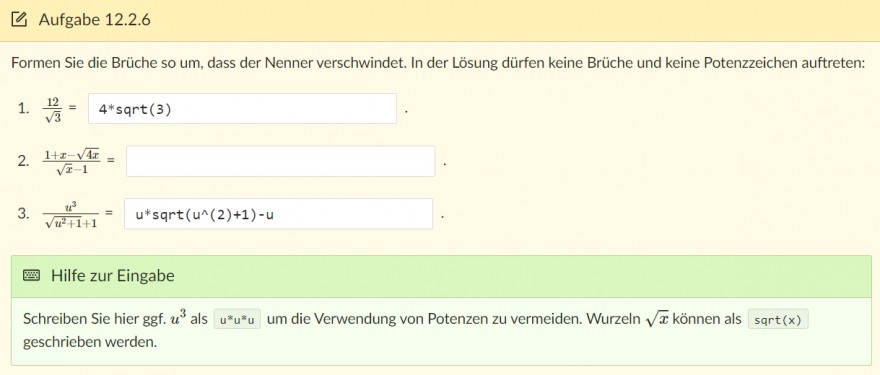
Formen Sie die Brüche so um, dass der Nenner verschwindet. In der Lösung dürfen keine Brüche und keine Potenzzeichen auftreten:
1. \( \frac{12}{\sqrt{3}}=4 * \operatorname{sqrt}(3) \)
2. \( \frac{1+x-\sqrt{4 x}}{\sqrt{x}-1}= \)
3. \( \frac{u^{3}}{\sqrt{u^{2}+1}+1}=\mathrm{u}^{*} \operatorname{sqrt}\left(\mathrm{u}^{\wedge}(2)+1\right)-\mathrm{u} \)
菏 Hilfe zur Eingabe
als Schreiben Sie hier ggf. \( u^{3} \) als \( u^{*} u^{*} u \) um die Verwendung von Potenzen zu vermeiden. Wurzeln \( \sqrt{x} \) können als \( \operatorname{sqrt}(x) \) zu geschrieben werden.
Problem/Ansatz:
Kann man den zweiten Term überhaupt umformen?