Hallo:-)
Man kann sich auch mal den Spaß drauß machen und sich ein Bildchen zu malen. Aber dafür forme ich zunächst folgende Gleichung (für positive \(a\)) etwas um:
$$ 1=\frac{x}{x^3-a}\quad \Leftrightarrow\quad x^3-a=x\quad \Leftrightarrow \quad x^3=x+a $$
Skizze:
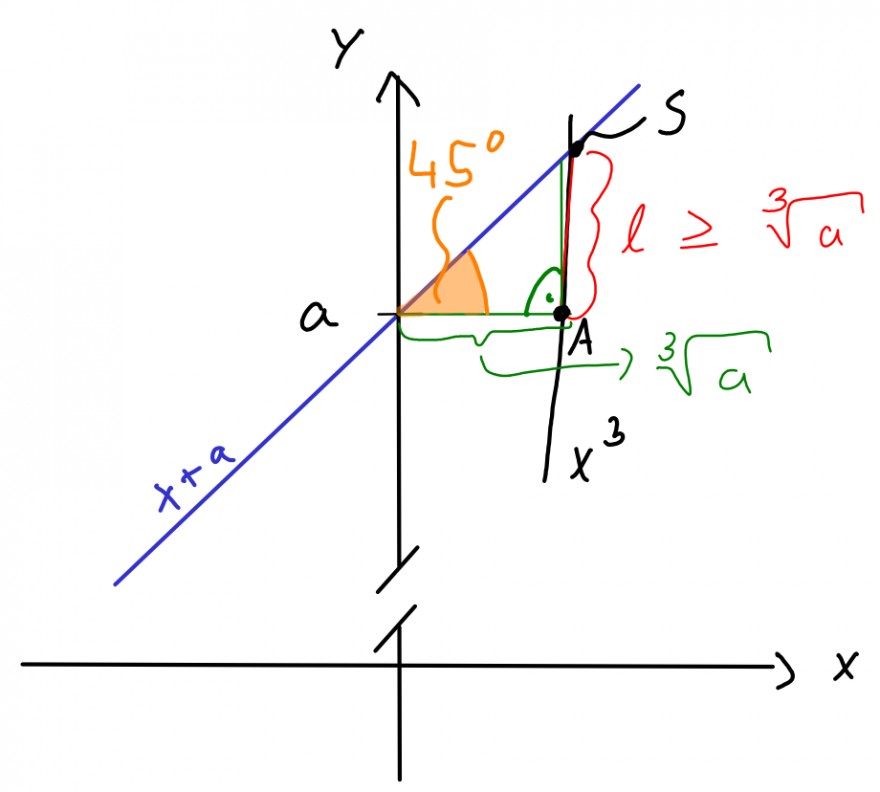
Links neben der Strecke \(\overline{AS}\) ist eine grüne Senkrechte, die durch den Punkt \(S=(x_S,y_S)\) geht. Diese schneidet die blaue Gerade bei \(\sqrt[3]{a}\). Jetzt kannst du dir mal bildlich vorstellen, was passiert, wenn du \(a\) immer größer wählst: Die grüne Senkrechte und die rote Strecke stimmen zunehmend überein. Also ist \(x_S\approx \sqrt[3]{a}\) für große Werte von \(a\) eine recht gute Näherungslösung für die Gleichung \(x^3=x+a\).
Testen wir mal: \(x_S\approx \sqrt[3]{365}\approx 7.14657\). Also
\(365\approx x_S^3=x_S+a\approx 7.14657+365=372.14657\).
Das Ergebnis kann man jetzt noch durch folgende geometrische Betrachtung verbessern:
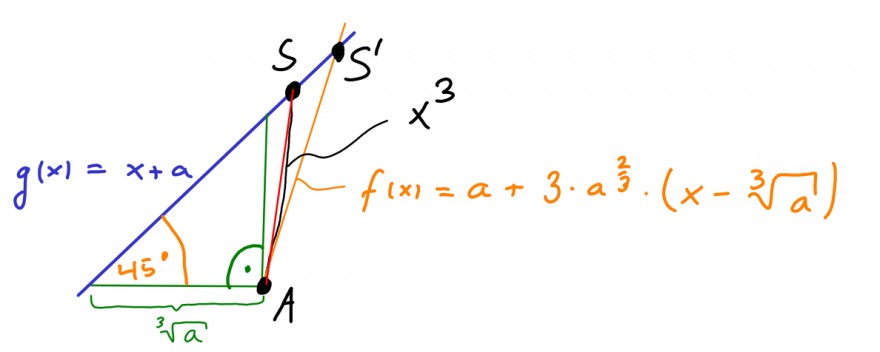
Statt die grüne Senkrechte, betrachte ich eine Tangente \(f\) von \(x^3\) im Punkt \(A=(\sqrt[3]{a},a)\). Erhöhe ich nun wieder \(a\), so wandert der Schnittpunkt \(S'\) beider Geraden \(f\) und \(g\) in den Punkt \(S\). Die \(x-\) Komponente von \(S'\) lautet:
$$ \begin{aligned}x+a=g(x)&=f(x)=a+3\cdot a^{\frac{2}{3}}\cdot (x-\sqrt[3]{a})\\\Leftrightarrow \qquad x&=3\cdot a^{\frac{2}{3}}\cdot (x-\sqrt[3]{a})=3\cdot a^{\frac{2}{3}}\cdot x-3\cdot a\\\qquad \Leftrightarrow (1-3\cdot a^{\frac{2}{3}})\cdot x&=-3\cdot a\\ \Rightarrow \qquad x&=\frac{3\cdot a}{3\cdot a^{\frac{2}{3}}-1}\geq \frac{3\cdot a}{3\cdot a^{\frac{2}{3}}}=a^{\frac{1}{3}}=\sqrt[3]{a}\end{aligned} $$
Also kann man daraus schonmal eine Einschränkung zum Lösen vornehmen:
\(x_S\in \left[\sqrt[3]{a},\frac{3\cdot a}{3\cdot a^{\frac{2}{3}}-1}\right]\).
Für \(a=365\) bekommst du so näherungsweise \(x_S\approx \frac{3\cdot a}{3\cdot a^{\frac{2}{3}}-1}\approx 7.19352\).
Testen wir mal: Also
\(372.24114\approx x_S^3=x_S+a\approx 7.19352+365=372.19352\). Das sieht doch schonmal besser aus.