Was lässt sich über die Ableitung der zugehörigen Funktion aussagen?

Question

Aufgabe:

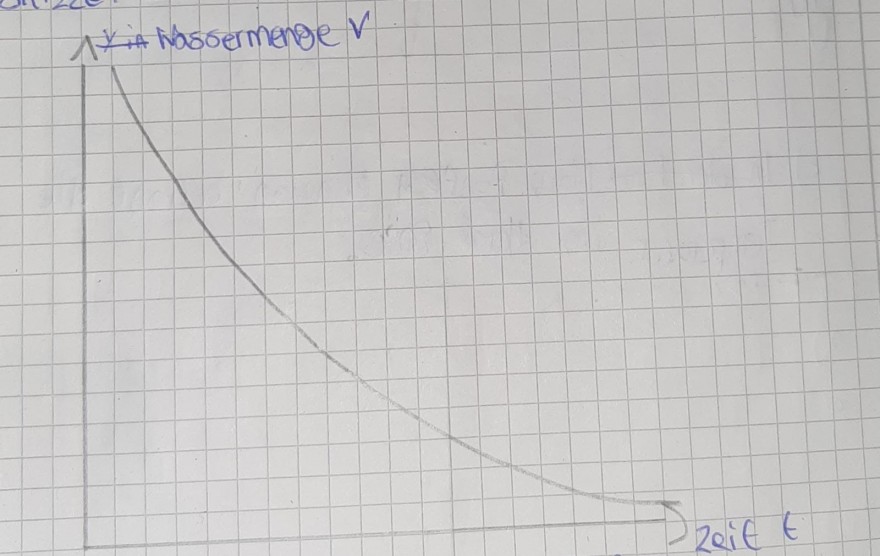
Eine Badewanne wird mit Wasser gefüllt. Nach dem Baden wird der Stöpsel gezogen und die Wanne läuft leer. Skizzieren Sie einen Graphen für die Wassernenge in der Wanne in Abhängigkeit von der Zeit. Was lässt sich über die Ableitung der zugehörigen Funktion aussagen?

Ansatz - Ist die Lösung richtig?

Der Graph ähnelt einer Expnentialfunktion. Dieser wiederum abgeleitet müsste dann wieder eine Exponentialfunktion sein. Denn bei einer Exponentialfunktion gibt es weder eine Nullstelle noch ein Extrema.

Answer 1

Hallo

deine Überlegung ist soweit richtig, ob es genau ne e funktion ist kann man nich t sagen, wenigstens nicht ohne Maßstab , das einzige was man genauer sagen kann auch f'  ist immer negativ, der Betrag von f' nimmt mit der Zeit ab, also ist f' negativ und wachsend . (wie -e^-x) also zusätzlich zu deiner Erläuterung noch das Vorzeichen von f'

Gruß lul

Answer 2

Aloha :)

Die maximale Wassermenge, die pro Zeiteinheit durch den Abfluss läuft ist konstant. Das heißt, die Geschwindigkeit, mit der das Wasser abläuft ist konstant. Eine halbvolle Wanne braucht die Hälfte der Zeit zum Ablaufen wie eine ganz volle Wanne. Die Funktion muss also eine fallende Gerade sein. Die Ableitung ist konstant und negativ.