ich sitze vor folgender Aufgabe:
a) Erstellen Sie zwei Schieberegler \( a_{1} \) und \( a_{2} \) für eine ganze Zahl in einem sinnvollen Intervall.
b) Verifizieren Sie mithilfe eines wahr-falsch-Berichts, dass für die ganzen Zahlen \( a_{1} \) und \( a_{2} \)
gilt: \( \left(a_{1}, a_{2}\right) \cdot\left[a_{1}, a_{2}\right]=\left|a_{1} \cdot a_{2}\right| \)
c) Lassen Sie sich den Zusammenhang \( \left(a_{1}, a_{2}\right) \cdot\left[a_{1}, a_{2}\right]=\left|a_{1} \cdot a_{2}\right| \) mittels eines dynamischen Textes in der Grafik-Ansicht anzeigen.
Ihr Ergebnis sollte in etwa wie folgt aussehen:
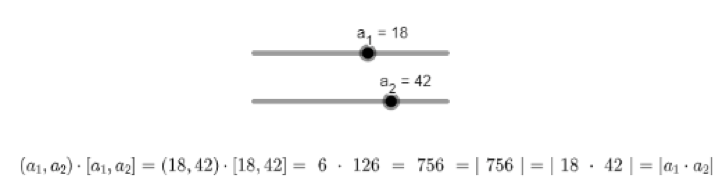
Text erkannt:
\( \left(a_{1}, a_{2}\right) \cdot\left[a_{1}, a_{2}\right]=(18,42) \cdot[18,42]=6 \cdot 126=756=|756|=|18 \cdot 42|=\left|a_{1} \cdot a_{2}\right| \)
Also die Aufgabe an sich verstehe ich, also was gezeigt werden soll. Ich kann nur einfach nicht mit diesem wahr-falsch-Bericht in Geogebra umgehen.. Ich bin wirklich dankbar, wenn mir hier jemand helfen könnte