Nullstelle von e-Funktion berechnen

Question

Aufgabe:

3-e^x=2/e^x

Nullstelle berechnen

Problem/Ansatz:

Ich weiss nicht, wie ich das machen könnte... Bitte in klaren Schritten zeigen

Comments

Das ist eine Gleichung. Gleichungen haben keine Nullstellen. Das wirft die Frage auf, was du eigentlich willst.

Answer 1

mal e^x:

3e^x -e^(2x)-2=0 |*(-1)

e^(2x)-3e^x+2=0

e^x= z

z^2-3z+2=0

(z-2)(z-1)=0

z=2 v z= 1

e^x= 2

x= ln2

e^x= 1 = e^0

x= 0

L= {0, ln2}

Answer 2

Hallo,

Du suchst die Schnittpunkte:

S1(0/2)

S2(ln(2(/1)

Comments

Danke ;) sehr hilfreich

Answer 3

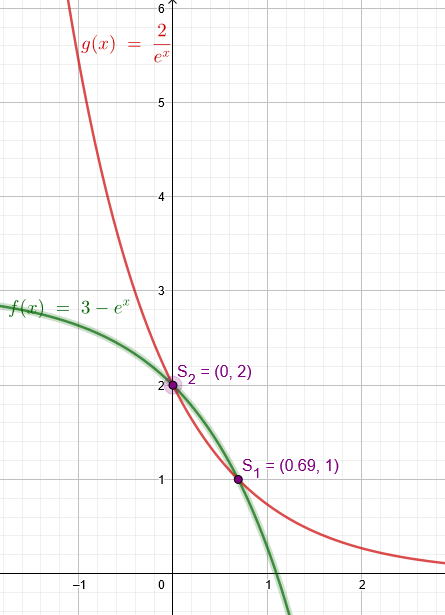
Die Aufgabe lautete wahrscheinlich:

f(x)=3-\( e^{x} \)

g(x)=\( \frac{2}{e^x} \)

Berechne die Schnittpunkte der beiden Funktionen:

3-\( e^{x} \) =\( \frac{2}{e^x} \)

3\( e^{x} \)-\( e^{2x} \)-2=0

\( e^{2x} \)-3\( e^{x} \)=-2

(\( e^{x} \)-1,5)^2=-2+2,25=0,25|\( \sqrt{} \)

1.)\( e^{x} \)-1,5=0,5

\( e^{x} \)=2

x₁=ln2≈0,69       y₁=3-\( e^{ln2} \)=3-2=1

2.)\( e^{x} \)-1,5=-0,5

\( e^{x} \)=1
x₂=ln1=0      y₂=\( \frac{2}{e^0} \)=\( \frac{2}{1} \)=2