Hallo,
betrachte das 1. Glücksrad. Blau hat einen Anteil von \( \frac{1}{2} \), gelb und grün jeweils \( \frac{1}{4} \).
"Zweimal dieselbe Farbe" bedeutet die Kombinationen blau-blau, gelb-gelb und grün-grün.
Entlang der Pfade wird multipliziert, die Ergebnisse addiert.
blau-blau hat eine Wahrscheinlichkeit von \(\frac{1}{2}\cdot\frac{1}{2}=\frac{1}{4}\)
gelb-gelb hat eine Wahrscheinlichkeit von \(\frac{1}{4}\cdot\frac{1}{4}=\frac{1}{16}\)
grün-grün hat die gleiche Wahrscheinlichkeit
Insgesamt ergibt sich also \(\frac{1}{4}+\frac{2}{16}=\frac{3}{8}\)
Hierzu noch das Baumdiagramm:
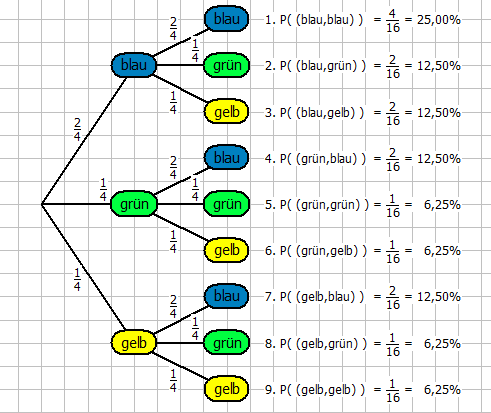
Wenn du das verstanden hast, solltest du auch die anderen Aufgaben lösen können. Sonst frage nochmal nach.
Gruß, Silvia