IAufgabe:
Problem/Ansatz:
Die Dachfläche kannst Du doch einfach geometrisch berechnen. Das sind zwei Trapeze und zwei gleichschenklige Dreiecke.
Die Trapeze haben parallele Seiten von 8 und 6 Einheiten Länge,dazu eine über den Satz des Pythagoras ermittelte Höhe von 5 Einheiten (Wurzel (4²+3²)).
Die Dreiecke haben eine Grundseite von 6 Einheiten und eine Höhe von Wurzel (1²+3²)=Wurzel (10).
Abstand Fahnenspitze zu J bekommst D, wenn Du die Differenzen der jeweiligen Koordinaten quadrierst, diese Quadrate addierst und aus der Summe die Wurzel ziehst.
Das war die Diskussion mit meinem Lehrer aber ich verstehe nicht wie ich das lösen soll und hier ist die Aufgabe
h)Zu einer bestimmten Tageszeit fällt ein Lichtstrahl auf den Fahnenmast in Richtung des Vektors ein. Berechnen Sie den Punkt J auf der Dachfläche BDE, auf den die Fahnenmastspitze abgebildet wird.[Zur Kontrolle: Auf zwei Nachkommastellen gerundet erhalten Sie J(-1,94|3,8|0,61).]
i)Berechnen Sie den Abstand des Punktes J vom Fahnenmast.
j)Berechnen Sie den Flächeninhalt der gesamten Dachfläche.
Hierzu ist der Text
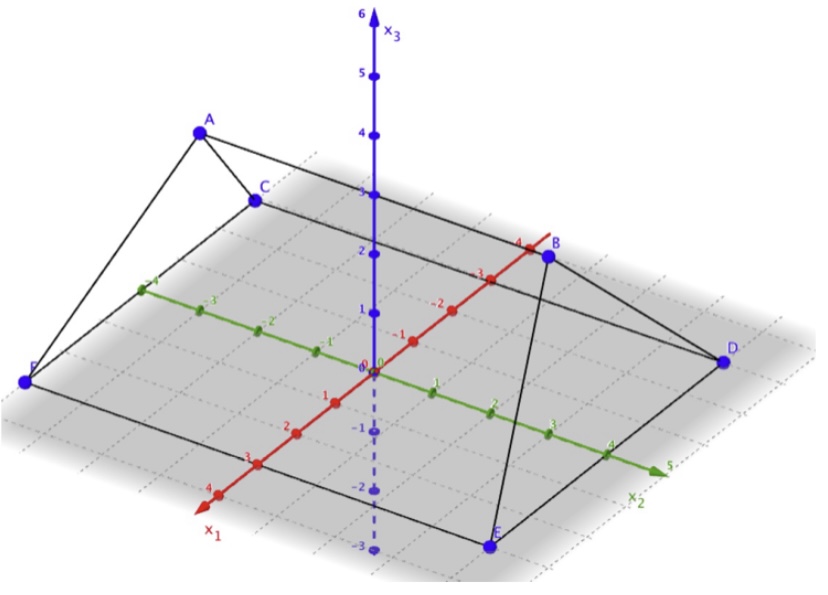
Aufgabe:Ein Haus erhält ein Walmdach der Form im Material 1. Die Punkte C, D, E und F
sind Eckpunkte des rechteckigen Dachbodens. Das Dach ist symmetrisch zur
x1-x3-Ebene. Eine Längeneinheit entspricht einem Meter. Gegeben sind die Punkte
A(0|-3|3), C(-3|-4|0), D(-3|4|0) und F(3|-4|0).
Und das sind die Koordinaten :
J(-1,94|3,8|0,61)
Mein Problem ist es dass ich schon die ganze Zeit an dieser Aufgabe sitze und ich habe meinen Lehrer gefragt und das war seine Antwort ich kriege die Aufgaben einfach nicht gelöst die gesuchten Koordinaten habe ich dazu gefunden die habe ich auch eingegeben ich habe aber kein Plan von dem was er gerade schreibt kann mir bitte jemand helfen ich kriege die Aufgaben nicht gelöst
Hier ist noch das Bild dazu und ja ich weiß es wurde schon oft diese Aufgabe hier reingestellt aber ich komm einfach nicht mehr weiter und hoffe dass es hier übersichtlicher ist