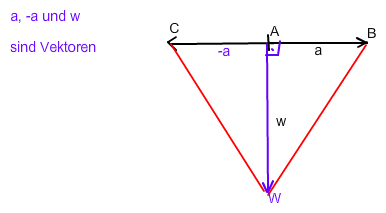
Zeichne einen beliebigen Vektorpfeil a = \(\overrightarrow{AB}\) , der in A beginnt und in B endet.
Der Gegenvektor -a = \(\overrightarrow{AC}\) zu a ist genau so lang wie a und hat die entgegengesetzte Richtung.
ΔBCW ist genau dann gleichschenklig , wenn der Vektor w = \(\overrightarrow{AW}\) senkrecht zur Strecke CB ist.
Die Länge von Vektor w ist beliebig.
Gruß Wolfgang