Quadratische Bezierkurve berechnen

Question

Aufgabe: Wie berechnet man die quadratische Bezierkurve zu dem Beispiel: A=(2,0) B=(4,2) C=(0,1)

…

Problem/Ansatz: ich kenne die Formel B(t)=(1-t)^2*b_0+2*t*(1-t)*b_1+t^2*b_2 , aber wie komme ich auf die Koeffizienten? Das Einsetzprinzip funktioniert schlecht bei 3 Variablen.

Comments

aber wie komme ich auf die Koeffizienten?

die drei Koeffizienten \(b_{0,1,2}\) SIND die drei Punkte \(A\), \(B\) und \(C\)

Das Einsetzprinzip funktioniert schlecht bei 3 Variablen

was hättest Du denn wo eingesetzt?

Answer 1

Du hast das Bernstein-Polynom ja schon aufgestellt: Mit Deinen 3 Punkten

\( q(t):=\left(1 - t \right)^{2} \; A + 2 \; t \; \left(1 - t \right) \; B + t^{2} \; C\)

in Geogebra

lagerst Du die x,y Koordinaten in je eine Funktion aus: etwa

B_x(t):=Sum({(-t + 1)², 2t (-t + 1), t²} {x(A), x(B), x(C)})

B_y(t):=Sum({(-t + 1)², 2t (-t + 1), t²} {y(A), y(B), y(C)})

q(t):=Curve(B_x(t), B_y(t), t, 0, 1)

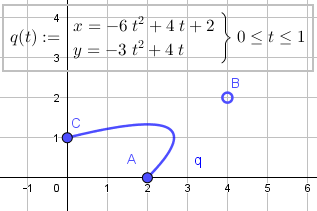
B ist Steuerpunkt der Kurve

Zur Konstruktion

https://www.geogebra.org/m/bm7veryu