Determinanten-Formel für eine Matrix finden

Question

Aufgabe:

Folgende Matrix ist gegeben

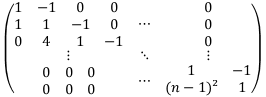
\( \left(\begin{array}{ccccccc}1 & -1 & 0 & 0 & & 0 & \\ 1 & 1 & -1 & 0 & \cdots & 0 & \\ 0 & 4 & 1 & -1 & & 0 & \\ & & \vdots & & & \ddots & \vdots & \\ & 0 & 0 & 0 & & \cdots & 1 & -1 \\ & 0 & 0 & 0 & & \cdots & (n-1)^{2} & 1\end{array}\right) \)

a) Finde eine Formel für \( \operatorname{det}\left(A_{n}\right) \) für \( n \geq 3 \)

b) Beweise \( \operatorname{det}\left(A_{n}\right)=n ! \)

Problem/Ansatz:

Bei dieser Matrix versuche ich mit dem Laplace stufenweise zu entwickeln, aber komme damit nicht weiter und bei der Beweisen-Aufgabe weiß ich nicht man das macht. Ausprobieren zählt nicht als beweisen, oder?

Comments

Entwicklung nach der letzten Zeile liefert$$\det(A_{n+1})=\det(A_n)+n^2\cdot\det(A_{n-1}).$$Weiter geht's mit Induktion über \(n\).