Bestimmen sie die Koordinaten der Punkte bei Spiegelung an der

Question

Aufgabe:

Gegeben sind die Punkte A(-1/2/0), B(0/3/0) und C(2/4/-1).

a) Die Punkte A,B,C werden an den Koordinatenebenen gespiegelt. Bestimmen sie die Koordinaten der Punkte bei Spiegelung an der

- x1x2-Ebene    - x1x3-Ebene    -x2x3-Ebene

Problem/Ansatz:

Ich kann mir das nicht so wirklich grafisch vorstellen kann mal bitte jemand eine Grafik von diesen Punkten reinstellen und diese Spiegelung darin zeigen?

danke voraus!

Answer 1

Besichtigung von Spiegelungen siehe

https://www.geogebra.org/classic/rmpcwjyv

Deine Ebenen müssten mit

E_1:x=0

E_1:y=0

Also als Abbildung

\(\small SE_{y=0} \, : \, \left(\begin{array}{rrr}1&0&0\\0&-1&0\\0&0&1\\\end{array}\right) A = \left(\begin{array}{r}-1\\-2\\0\\\end{array}\right) \)

E_1:z=0

Grundsätzlich gehst Du senkrecht auf die Ebene und den gleichen abstand auf die "andere" Seite

Answer 2

Hallo,

Spiegelung an der xy-Ebene: Hier kannst du nur den Punkt C spiegeln, da die anderen beiden Punkte in dieser Ebene liegen:

Spiegelung an der xz-Ebene:

Spiegelung an der yz-Ebene - hier nur A und C:

Gruß, Silvia

Answer 3

Hallo,

Ich kann mir das nicht so wirklich grafisch vorstellen kann mal bitte jemand eine Grafik von diesen Punkten reinstellen und diese Spiegelung darin zeigen?

Als Beispiel habe ich das mit dem Punkt \(C\) gemacht, dessen drei Kordinaten ungleich 0 sind. Du siehst hier den Punkt \(C\) und seine drei Spiegelbilder an den drei Koordinatenebenen.

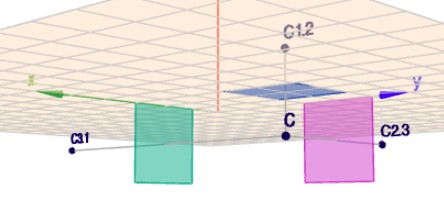
Der Punkt \(C\) liegt unterhalb der horizontalen \(x_1x_2\)-Ebene (alias XY-Ebene). Ich habe Dir quadratische Flächen der drei Ebenen heraus gezeichnet, so dass es klarer wird.

Klick bitte auf das Bild oben. Dann öffnet sich Geoknecht3D und Du kannst die Szene mit der Maus drehen und bekommst so einen guten räumlichen Eindruck.

Melde Dich bitte, wenn was nicht klar ist.

Gruß Werner