Bestimmen Sie die Ableitung der Funktion, berechnen Sie N' (t) = 1 und interpretieren Sie den berechneten Wert.

Question

Aufgabe:

Aufgabe: In einem Labor mit einer Raumtemperatur von 20 °C wird zum Zeitpunkt t= 0 eine Flüssigkeit aus dem Kühlschrank genommen und im Labor abgestellt. Daraus ergibt sich die Funktionsgleichung N(t)=20-15e^-0,2231t.  a)Ermitteln Sie, nach wie vielen Minuten sich die Flüssigkeit auf 15 °C erwärmt hat. b) Zeichnen Sie den Graphen der Funktion für die ersten 10 Minuten in ein Koordinatensystem. c) Bestimmen Sie die Ableitung der Funktion, berechnen Sie N' (t) = 1 und interpretieren Sie den berechneten Wert.

Problem/Ansatz:wie muss man vorgehen + lösung ?

Answer 1

Hallo,

Text erkannt:

\( \begin{array}{l} N(t)=20-15 e^{-0,2231 t} \\ N^{\prime}(t)=3,3465 e^{-0,2231 t} \end{array} \)

a)

\( \begin{array}{l} 15=20-15 e^{-0,2231 t} \\[10pt] -5=-15 e^{-0,2231 t} \\[10pt] \frac{1}{3}=e^{-0,2231 t} \\[10pt] \ln \left(\frac{1}{3}\right)=-0,2231 t \\[10pt] 4,92=t \end{array} \)

b)

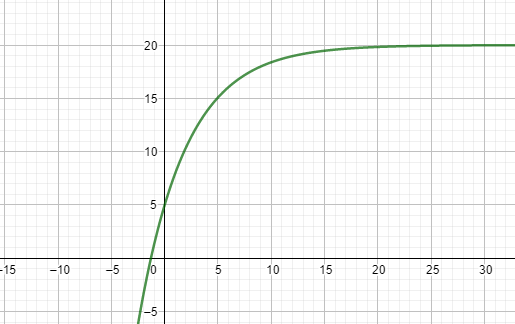
c) \( N^{\prime}(1)=3,3465 e^{-0,2231} \approx 2,68 \)

Comments

bei nr. c muss man doch N'= 1 und nicht von eins rechnen?

---

Oh ja, da habe ich mich vertan.

\( \begin{aligned} 3,3465 e^{-0,2231 t} &=1 \\ e^{-0,2231 t} &=0,29882 \\-0,2231 t &=ln(0,29882) \\-0,2231 t &=-1,2079 \\ t &=5,41 \end{aligned} \)