Schreibe in Excel in die Zelle A1 irgendeine Zahl (nur nicht 0).
Schreibe in die Zelle A2 die Formel
=7-10/A1
Übertrage diese Formel nach A3, A4, A5 usw. (bis A20 sollte genügen.)
Sieh dir die Entwicklung der Werte von A1 bis A20 durch. Vermutest du Konvergenz?
Probiere nun in der Zelle A1 andere Werte aus und schau auch dort auf mögliche Konvergenz.
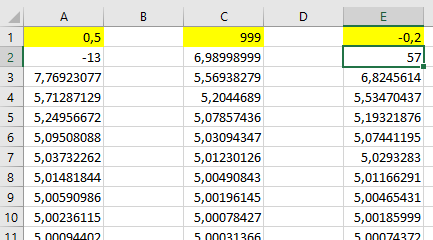
Die Abbildung zeigt die ersten 10 Werte mit den Startwerten 0,5 bzw. 999 bzw. -0,2. Da liegt offensichtlich Konvergenz vor. Du kannst ja aber noch selbst einfachere Startwerte wie 1, 2 oder 3 versuchen.