Kurze Antwort: Ja, die Grenzen sind richtig, ich vermute, dass du vielleicht nicht mit dem Betrag der Jacobi-Matrix im Integral multiplizierst und du deswegen nicht zum gewünschten Ergebnis kommst.
Ganze Lösung:
Bei solchen Aufgaben ist es immer empfehlenswert, zuerst eine Skizze zu machen:
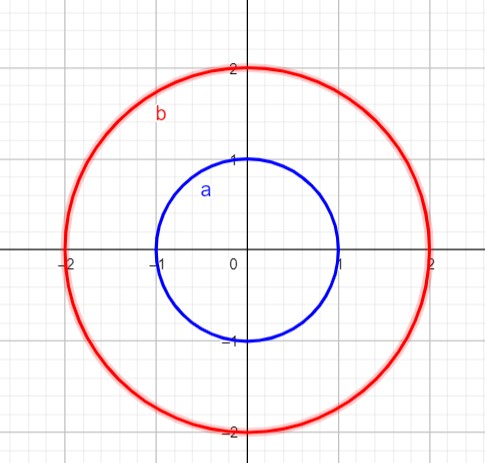
Alle Punkt innerhalb des roten Kreises erfüllen x^2+y^2<=4 und alle Punkte außerhalb des blauen Kreises 1<=x^2+y^2. x,y>=0 schränkt den Bereich weiter auf den ersten Quadranten ein. Wir suchen also die Fläche des Viertels des Kreisrings, das rechts oben liegt.
1. Methode grafisch:
Wir setzen einfach in die Formel für den Flächeninhalt von einem Kreisring ein und teilen anschließend durch 4:
$$A_{Kreisring}=\pi\cdot(r_{außen}^2-r_{innen}^2)=\pi\cdot(2^2-1^2)=3\pi$$
Nun dividieren wir noch durch 4, weil wir ja nur ein Viertel des Kreisringes wollen:
$$3\pi:4=\frac34\pi$$
2. Methode Integral:
Wir transformieren, zu Polarkoordinaten:
$$(x,y)^T=(r\cdot \cos(\varphi), r\cdot \sin(\varphi))^T$$
Nun bestimmen wir die Intervalle über die wir, r und phi integrieren. Der Radius von r ist beim inneren Kreis am kleinsten, also 1 und am äußeren Kreis am größten, also bei 2. Es gilt deswegen: r liegt in [1,2]. Phi läuft wie vorher gesagt über das Viertel oben rechts, also von 0 bis pi/2 (90°).
Hierbei handelt es sich um ein zweidimensionales Integral, wir brauchen also ein Doppelintegral über 1 (wir haben die beiden Variablen, also passt das). Beim Transformieren muss man immer noch mit dem Betrag der Jacobi-Matrix multiplizieren. Bei gewöhnlichen Polarkoordinaten ist das einfach der Radius r.
Nun können wir integrieren:
$$\begin{aligned}&\int_{0}^{\pi/2}\int_1^{2}\underbrace{r\cdot drd\varphi}_{dxdy}=\int_{0}^{\pi/2} \dfrac12\left[r^2\right]_{1}^2\,d\varphi=\int_{0}^{\pi/2} \dfrac12 (4-1)\,d\varphi=\dfrac{3}{2}\int_{0}^{\pi/2}1\,d\varphi=\dfrac{3}{2}[\varphi]_0^{\pi/2}=\dfrac{3}{4}\pi\end{aligned}$$