Bestimmen Sie das Bild \mu_{A}(M) der Menge M:=\left\{x ∈ ℝ^{2} ; 1 ≤ x_{1} ≤ 2,-1 ≤ x_{2} ≤ 1\right\} .

Question

Wie muss ich da vorgehen?

Vorgelegt sei die Matrix
\( A:=\left[\begin{array}{cc} -2 & 3 \\ 2 & -1 \end{array}\right] \in \mathbb{R}^{2 \times 2} \text {. } \)
Außerdem bezeichne \( \mu_{A}: \mathbb{R}^{2} \rightarrow \mathbb{R}^{2} \) die von \( A \) durch \( \mu_{A}(x):=A \cdot x \) erzeugte lineare Abbildung.
a) Bestimmen Sie das Bild \( \mu_{A}(M) \) der Menge \( M:=\left\{x \in \mathbb{R}^{2} ; 1 \leq x_{1} \leq 2,-1 \leq x_{2} \leq 1\right\} \).

Answer 1

Aloha :)

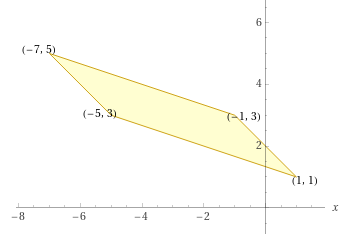
Wir lassen die Matrix \(A\) auf einen Punkt \((x_1|x_2)\) wirken:$$A\binom{x_1}{x_2}=\left(\begin{array}{rr}-2 & 3\\2 & -1\end{array}\right)\binom{x_1}{x_2}=x_1\left(\begin{array}{r}-2\\2\end{array}\right)+x_2\left(\begin{array}{r}3\\-1\end{array}\right)$$

Wegen \(1\le x_1\le2\) und \(-1\le x_2\le1\) entsteht ein Parallelogramm mit den Eckpunkten:$$A\binom{1}{-1}=\binom{-5}{3}\quad;\quad A\binom{1}{1}=\binom{1}{1}\quad;\quad A\binom{2}{-1}=\binom{-7}{5}\quad;\quad A\binom{2}{1}=\binom{-1}{3}$$

Comments

wow, vielen Dank :) Sehr verständlich