Punktweise Definition einer Kurve

Question

Es gibt Hunde, die aggressiv werden, sobald sie einen Radfahrer entdecken. Warum das so ist, soll hier nicht untersucht werden. Vielmehr interessiert uns die Frage, welche Chance ein Radfahrer hat, einem aggressiven Hund zu entkommen. Dazu stellen wir uns folgende Ausgangssituation vor:

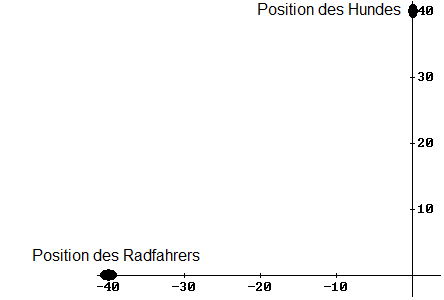
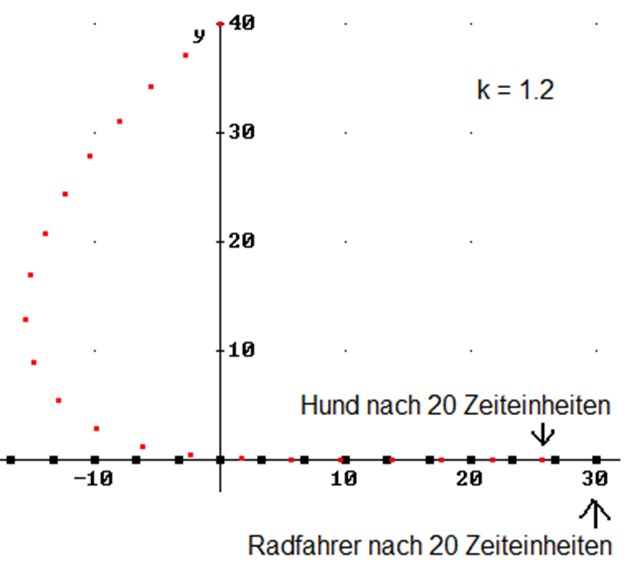
Auf einer ebenen Fläche mit freier Sicht bewegt sich der Radfahrer auf der x-Achse mit konstanter Geschwindigkeit vom Punkt (-40/0) zum Punkt (0/0) und, wenn es gelingt dem Hund zu entkommen, auch darüber hinaus. Der Hund startet in der Position (0/40) als er den Radfahrer in dessen Position (-40/0) entdeckt und ist nicht so intelligent, dem Radfahrer den Weg abzuschneiden. Vielmehr springt er in 4 m langen Sätzen und mit konstanter Geschwindigkeit immer genau auf die jeweilige, sich verändernde Position des Radfahrers zu. Haben Hund und Radfahrer die gleiche Geschwindigkeit, erreicht der Hund den Radfahrer auf Grund seiner verfehlten Verfolgungstaktik nie. Sollte der Hund schneller sein, als der Radfahrer, würde er das Rennen schließlich auch mit der verfehlten Taktik gewinnen. Aber der Hund gibt nach 20 Sätzen auf, falls er den Radfahrer bis dahin nicht erreicht hat. Bei welchem Geschwindigkeitsverhältnis hat der Radfahrer die Chance, dem Hund zu entkommen?

Den Zeittakt wählen wir so, dass ein Satz des Hundes genau eine Zeiteinheit dauert. Der Hund habe die k-fache Geschwindigkeit des Radfahrers mit k > 1, damit er überhaupt eine Chance hat. Die Positionen von Hund (H) und Radfahrer (R) zu einem Zeitpunkt t werden durch folgende Skizze veranschaulicht:

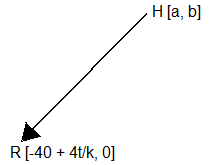
Die Position des Radfahrers ändert sich nur in der x-Koordinate, für die der Ausdruck
#1    – 40 + 4t/k
geschrieben wird. Die Strecke (oder auch der Pfeil) von H nach R heißt dann: [#1, 0] – [a, b] = [#1 – a, – b]. Damit diese Strecke die Länge des Satzes des Hundes erhält, muss sie zunächst durch ihre eigene Länge dividiert und dann mit 4 (jeder Satz ist 4 m lang) multipliziert werden. Dies leistet insgesamt der Faktor:
#2 4/BETRAG([#1 – a, – b]).
Der von [a, b] ausgehende Satz ist dann #2∙[#1 – a, – b] und da dieser von [a, b] ausgeht, endet er bei [a, b] + #2∙[#1 – a, – b] =  [a + #2∙(#1 – a), b – #2b]. In diesem Vektor brauchen wir eine dritte Komponente t + 1, welche von einem Satz zum nächsten weiterzählt. Per Rekursion wird nun zu [a, b, t] der unmittelbare Nachfolger [a + #2∙(#1 – a), b – #2b, t + 1] gefunden:

Beginne mit [0,40,0]

WIEDERHOLE: [a, b, t]→[a + #2∙(#1 – a), b – #2b, t + 1],

20 Wiederholungen

Daraus muss zum Zeichnen die Zeitzählkomponente wieder entfernt werden. Die Punkte, auf denen der Hund nach jedem Satz landet; sind in der folgenden Skizze rot: